問 題
最小二乗法に関する次の記述の ㋐、㋑、㋒ に当てはまるものの組合せとして最も妥当なのはどれか。
「ある実験で二つの量 x、y を測定したところ、n 組の測定値(xi、yi)(i = 1、2、…、n)が得られた。x、y の関係が y = ax + b で表されると仮定し、最小二乗法を用いてa、b を求めることを考える。すなわち、次の式で表される残差平方和 S を最小にする a、b を求める。
S = ㋐
そのためには、まず、次のように、S を a、b それぞれで偏微分して 0 とおく。
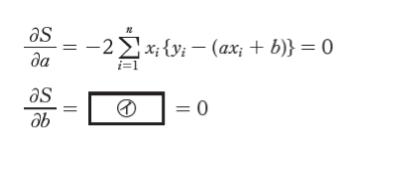
これらの式から、次の連立方程式が得られる。
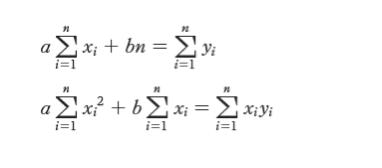
これより、a、b は次のように求められる。
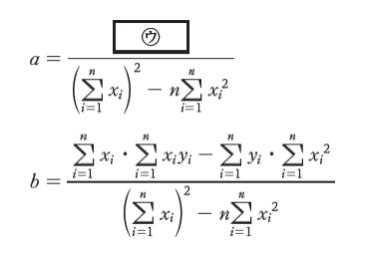
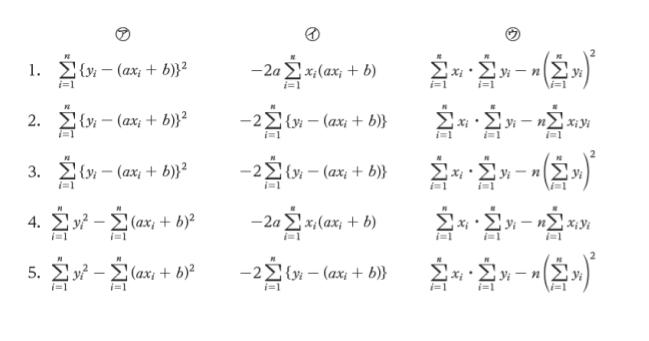
解 説
「最小二乗法…なんだったっけ、なんか文字がいっぱいだしいやだな..」といった印象を受けた人はぜひ「具体的に考える」とよいです!
a = 1, b = 1, n = 2 とします。すると x,y の関係は y = x + 1 です。データとして、完璧に直線で表せる簡単な例として (x1,y1) = (1,2)、(x2,y2) = (2,3) を考えます。そうすると、かなりイメージがわきやすいのではないでしょうか。

㋐ ですが
選択肢 を具体的な数で考えれば「{y1 – (x1 + 1)}2 + {y2 – (x2 + 1)}2」・・・(1) か「y12 + y22 -((x1 + 1)2 + (x2 +1)2)」・・・(2) のどちらかです。「残差平方和」という字面から「差の平方の和」と読むのが自然です。すると 差をとってから 2 乗している (1) の式を示唆すると考えられます。
また、具体的に考えることで (1) の式がやろうとしていることは「y1 の値と x1 + 1 の値の差を出して 2乗する、y2 の値と x2 + 1 の値の差を出して 2乗する …」と読み取れるのではないでしょうか。そうすると、この差がすごく小さくなるような直線 ax + b を考えれば、測定値の x,y の関係を表す式と言えそうです。これらの推測から ㋐ は (1) で、正解は 1 ~ 3 です。
㋑ については 偏微分ができないと判断ができないので、知らなかったり自信なければ飛ばして大丈夫です。また、具体的に考えると偏微分もやりやすいと思われます。㋑ について計算しなくても正解をしぼれます。
㋒ ですが
a = … を具体的に考えます。右辺の分母は既に書かれている式より「 (x1 + x2)2 – 2×(x12 + x22)」 となります。x1 = 1,x2 = 2 を代入すれば 9 – 10 = -1 です。a = 1 としているので、分子が -1 となるような式が正解です。
分子は (x1 + x2)・(y1 + y2) – 2 × (y1 + y2)2 ・・(1) か (x1 + x2)・(y1 + y2) – 2 × (x1y1 + x2y2) ・・・(2) のどちらかです。※太字部分のみが違いです
x1 = 1,x2 = 2,y1 = 2,y2 = 3 を代入して計算すれば (2) が妥当です。
従って、正解は 2 です。
以下は補足解説ーーー
㋑ の偏微分 及び
㋒ の連立方程式から a,b の導出過程について
補足として計算過程を示します。
公務員試験の得点力という観点からは、本文解説のように、具体的に考えて少しでも抵抗する考え方を身につけるのがおすすめです!
【㋑ について】
Σ を展開して和の形にしておくとわかりやすいです。
{y1 – ax1 – b}2 + {y2 – x2 – b}2 + …としておきます。
b で偏微分なので、b 以外は全て定数とみなします。
{-b + ◯}2 + {-b + △}2 +… という形ということです。これを b で微分すればよいです。2{-b + ◯} × (-1) + 2{-b + △} × (-1) + … となります。※ 合成関数の微分なので (-b + 定数)’ である 「-1」をかけるのを忘れないように!
従って、-2 を外に出した形である選択肢 (2,3,5) が正解となります。
【㋒ について】
㋒ の連立方程式について、Σ の項をそれぞれ c,d,e,f,g とおくと、以下のように「ac + bn = d と ae + bc = g」の連立方程式となります。
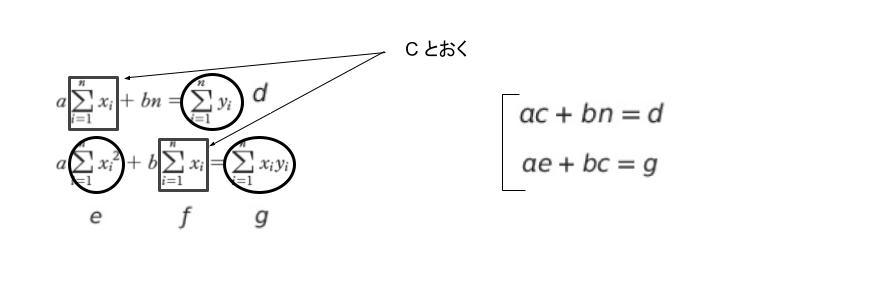
あとは加減法で a = … の形にすればよいです。一例として、以下のように計算して a = (cd – gn)/(c2 – ne) となります。

各文字を Σ に戻して選択肢と照らし合わせることで、正解を見つけることができます。
以上、補足解説終わりーー

コメント