問 題
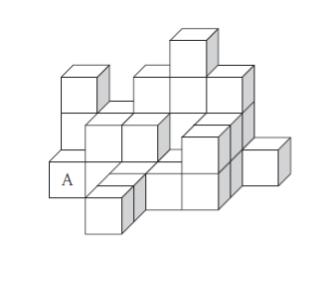
全面が白又は青のいずれか一色で塗られた同じ大きさの立方体が、合わせて 30 個ある。これらの立方体を、接する面どうしの色が異なるように積み上げ、図のような立体を作った。A の立方体の色が青であるとき、白の立方体の個数から青の立方体の個数を引いた数はいくらか。
1. 0
2. 1
3. 2
4. 3
5. 4
正解 (3)
解 説
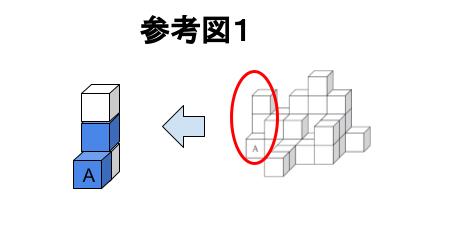
一列分ずつ見て決めていけばよいです。一番左端の列には立方体が4つあり、テトリミノの L 型の形で積まれています。A が青とのことなので、青→白→青→白です。参考図1参照。
次の列では、A と接している立方体は白となり、そこから全ての立方体の色が確定します。後は順に一列ごと見ていき、もれやずれがないよう、気をつけることができるかどうかがポイントになります。
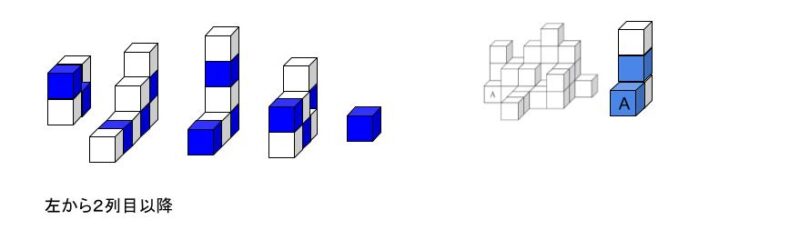
数えると、青14、白16です。16-14=2 となります。※選択肢の番号は3であることに注意しましょう!
以上より、正解は 3 です。

コメント