問 題
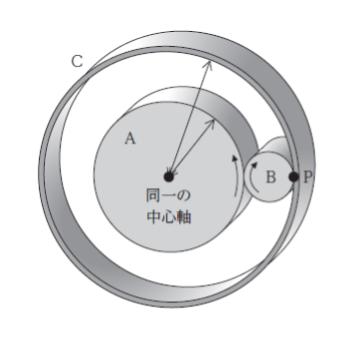
図のように、半径 3 の円筒Aと半径 1 の円筒 B が接しており、B は固定された円筒 C の内側と接している。A が中心軸を中心に回転すると、B は A と C に対して滑ることなく回転する。
はじめに C と接していた B 上の点 P が描く軌跡(太線)として最も妥当なのは次のうちではどれか。ただし、A と C の中心軸は同一であり、A と B の中心軸は平行であるものとする。
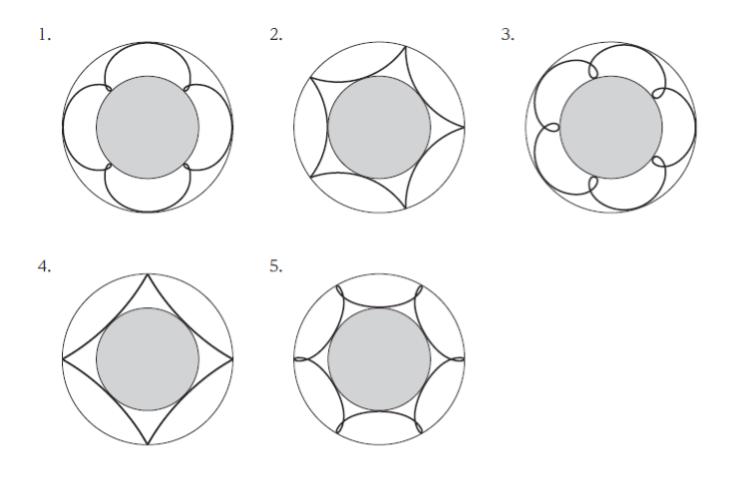
正解 (2)
解 説
軌跡なので、選択肢の消去法で考えます。
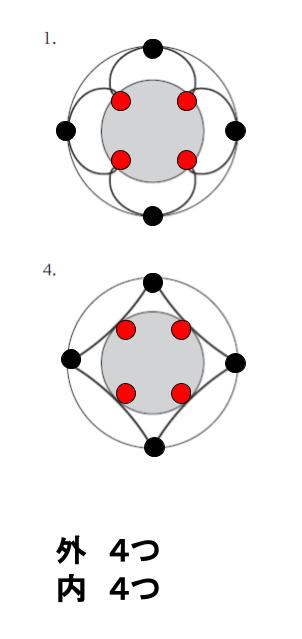
外側の円 及び 内側の円に接している点の個数が 選択肢 1,4 は4つ、選択肢 2,3 は 5 つ、選択肢 5 は 6 つです。選択肢 1,4 について下図参考。他の選択肢も同様です。
回転する B の円周は、半径が1 → 直径が2 → 円周が2π です。また、外側の円筒 C の円周は同様に考えると 半径が5 → 直径が10 → 円周が10πです。
10π ÷ 2π=5なので、B は元の場所に戻ってくるまでに5周します。したがって、外側 及び 内側の円に接する点の個数は5個と考えられます。選択肢 2,3 が正解の候補です。
後は1点に注目して、少しだけ動かしてみると判断しやすいかと思われます。選択肢 2,3 の大きな違いとして、内側の円筒と接している部分付近でくるりんと巻いているかどうかに注目します。このように、直前でくるりんと巻いたりしません。
ちなみに、この点の軌跡は「ハイポサイクロイド」です。動画などで動き方を見ておくと、同様の問題でイメージがわきやすいと思います。(参考 wiki の「Hypocycloid」の項目へのリンク)。
以上より、正解は 2 です。

コメント