2021年 国家一般職(高卒 技術) No.8 数学　解説

　問 題　　　　　

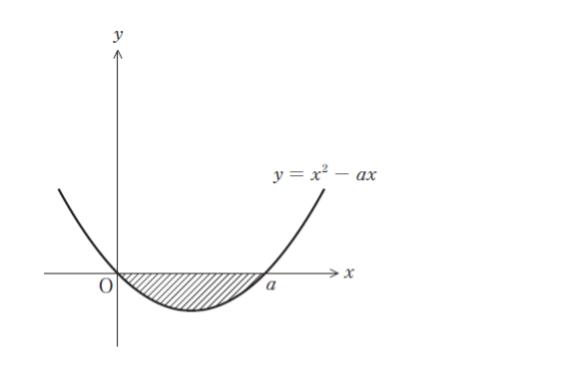
図のように、xy 平面上において曲線 y = x²– ax（a > 0）と x 軸で囲まれた領域の面積が 1/6 であるとき、定数 a はいくらか。

　

 

 

 

 

 

　解 説　　　　　

【解法１　定積分の計算】

斜線部の面積は、上端が y = 0、下端が y = x² – ax なので、以下のような定積分で表せます。

定積分を計算すると、a³/6 です。これが 1/6 になればよいので a = 1 です。

以上より、正解は 2 です。

※ a を含むため、積分が苦手なら避けた方がよい印象です。

【解法２　選択肢を活用、概算】

選択肢 1 が正解と仮定します。
a = 2/3 の時、頂点の x 座標は 1/3 です。x = 1/3 を x² – 2x/3 に代入すれば、y = -1/9 となります。下図のように表すことができます。

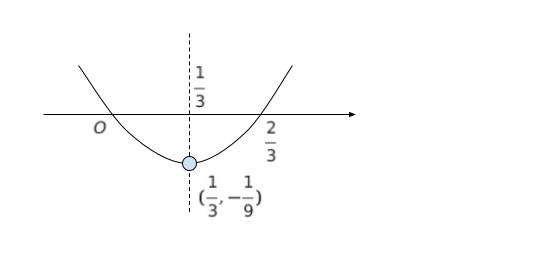
この時、斜線部の面積を三角形で近似すると、底辺 2/3 、高さ 1/9 なので 1/27 となります。下図のように近似して計算するということです。

少しはみ出した部分があるとはいえ、斜線部の面積は 1/6 にならないと考えられます。選択肢 1 は誤りです。以下、同様に各選択肢を正解と仮定して検討します。

選択肢 2 ですが
a = 1 の時、頂点は (1/2,1/4) です。斜線部の面積を三角形で近似すれば 1/8 です。1/6 に近いので保留します。

選択肢 3 ですが
a = 4/3 の時、同様に斜線部の面積を三角形で近似すれば、1/4 です。斜線部の面積はこれよりも大きいため、明らかに選択肢 3 は誤りです。また、以降の選択肢では、斜線部の面積がさらに大きくなるため、選択肢 4,5 も誤りです。

以上より、正解は 2 と判断できます。