問 題
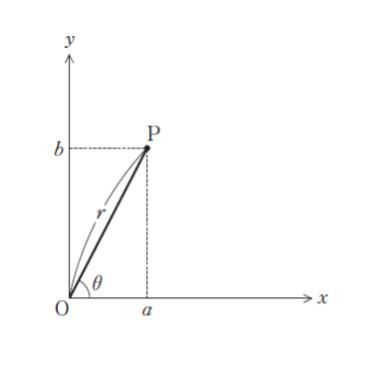
図のような xy 平面上において原点 O から r 離れた第 1 象限にある点 P の座標(a、b)を、r と θ(0° < θ < 90°)を用いて表したものとして正しいのはどれか。
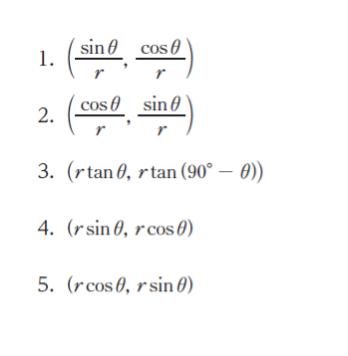
正解 (5)
解 説
座標 (a,b) の別の表し方として極座標表現というものがあります。原点からある点までの距離を r、x 軸から反時計回りに何度方向にあるかを偏角 θ とした時に、a = rcos θ、b = rsin θ と表す形式です。図形表現が簡潔にできるなどのメリットがある形式です。
以上より、正解は 5 です。
極座標形式に触れたことがなくても、r = 1、θ = 60° の時、(a,b) = (1/2、√3/2)。r = 2、θ = 60° の時、(a,b) = (1、√3)などを具体的に考えることで、正解は選べると思われます。
また、sin θ や cos θ の値についてぱっと浮かばない場合は H29 no4 解説 より 「単位円を用いた三角比の定義」をぜひ確認しておきましょう。

コメント