2021年 国家一般職(高卒 技術) No.3 数学　解説

　問 題　　　　　

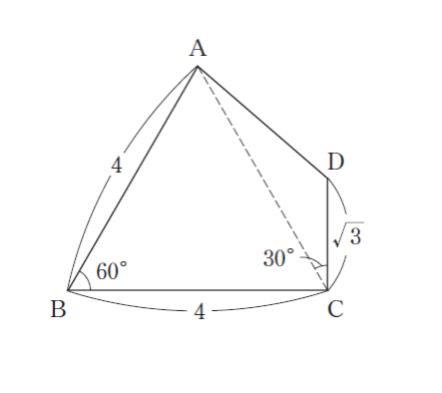
図のような AB = 4、BC = 4、CD = √3 、∠ABC = 60°、∠ACD = 30° の四角形 ABCD の面積はいくらか。　

 

 

 

 

 

　解 説　　　　　

△ ABC は、BA = BC の二等辺三角形 かつ、∠ B = 60° より、∠ A = ∠ C = 60° です。つまり、正三角形とわかります。

一辺 a の正三角形の面積は √3/4 a² です。これは基礎知識です。△ ABC は一辺 4 の正三角形なので、面積は 4√3 です。後は △ ACD の面積がわかればよいです。以下、２通りの解法を紹介します。どちらも場合に合わせて使えるようにすることをおすすめします。

 

【解法１：△ ACD の面積を概算】
△ACD は、△ ABC の半分 ＝ 4√3 ÷ 2 = 2√3 よりは小さいと評価できます（下図参照）。

そのため、四角形 ABCD は、△ ABC + 2√3 ＝ 6√3 よりも小さいと考えられます。そして、四角形 ABCD は △ ABC よりは明らかに大きいので、4 √3 よりは大きいです。つまり、4√3 ～ 6√3 の間が正解です。

以上より、正解は 2 です。

 

【解法２：補助線を引いて△ ACD の面積を計算】
点 D から AC に垂線を下ろし、交点を E とおきます。

△ DEC は 30°、60°、90° の直角三角形なので、辺の比が１：２：√３です。比で言う２が、長さ √3 なので、比で言う１に対応する DE = √3/2 とわかります。△ ACD の面積は、底辺を AC、高さを DE と見れば、1/2 × 4 × √3/2 = √3 です。

四角形 ABCD = △ ABC + △ ACD = 4√3 + √3 = 5√3 

以上より、正解は 2 です。