公務員試験 2021年国家一般職(土木) No.23 解説

　問題　　　　　

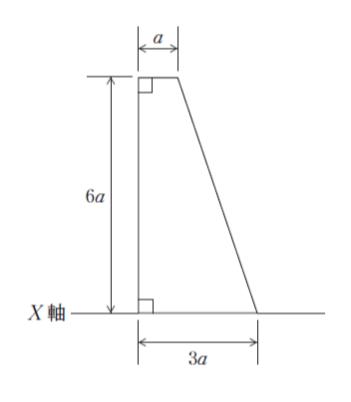
図のような断面の X 軸に関する断面二次モーメントはいくらか。

1． 102 a⁴2． 108 a⁴3． 114 a⁴4． 120 a⁴5． 126 a⁴

正解 (2)

　解説　　　　　

【断面二次モーメントの基礎知識】
・図心を通る軸に関する
三角形の断面二次モーメントは I = bh³/36 です。

・図心軸を通る軸に関する
長方形断面の二次モーメントは『図心軸方向を bとして bh³/12』です。

・図心を通らない場合の断面二次モーメントは
「図心を通る場合の断面二次モーメント」＋Ay² です。

※ A は断面積です。
※ y は軸から図心までの距離です。

台形を
長方形 (縦 6a、横 a) と三角形 (底辺 2a、高さ 6a) に分割します。

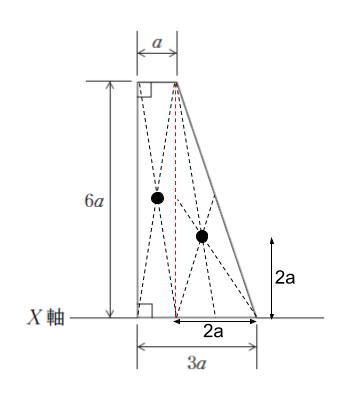
【長方形部分の断面二次モーメント】
長方形の図心は対角線の交点です。そのため、軸から図心までの距離 y = 3a です。b = a、h = 6a、A = 6a² を代入します。

a × (6a)³/12 + 6a² × (3a)²
= 72a⁴ ・・・(1)

【三角形部分の断面二次モーメント】
三角形の図心は中線の交点です。軸から図心までの距離 y = 2a です。b = 2a、h = 6a、A = 6a² を代入します。

2a × (6a)³/36 + 6a² × (2a)²
= 36a⁴ ・・・(2)

(1) + (2) = 108a⁴

以上より、正解は 2 です。

コメント