公務員試験 2021年 国家一般職(土木) No.22 解説

　問 題　　　　　

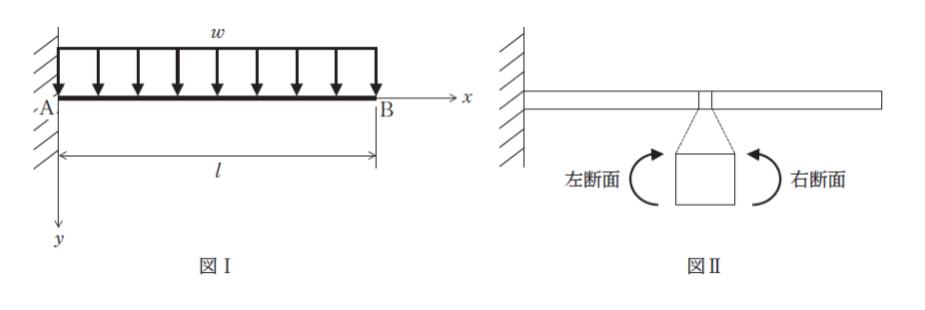
図Ⅰのように等分布荷重 w が作用し、曲げ剛性が EI で一様な片持梁がある。弾性曲線方程式を用いて梁の先端 B に生じる鉛直方向のたわみを求めるとき、次の記述の ㋐、㋑、㋒ に当てはまるものの組合せとして最も妥当なのはどれか。

ただし、曲げモーメントは、図Ⅱの向きを正とする。また、梁の自重は無視するものとし、変位は微小であるものとする。

「図Ⅰのように、固定端 A から水平右向きにx 軸、鉛直下向きにy 軸をとる。弾性曲線方程式は、任意の xにおける梁の鉛直方向のたわみ y (x)、曲げモーメント M(x)、EI を用いて

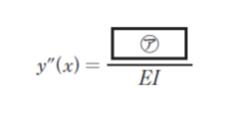
と表せる。さらに両辺を 2 回積分することで、y (x) は定数 C₁ 及び C₂ を用いて

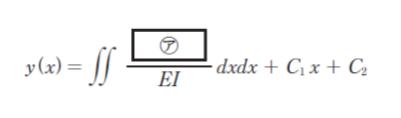
と表せる。ここで、考慮すべき境界条件は、y (0) = 0、 ㋑ であるから、C₁ 及び C₂ が求められる。したがって、B の鉛直方向のたわみは、y (x) = ㋒となる。」

 

 

 

 

 

　解 説　　　　　

㋐ ですが
梁のたわみ曲線の微分方程式は、水平右向きの座標を x、鉛直下向きのたわみを y、位置 x での曲げモーメントを Mx とすると 、梁の断面 2 次モーメント I、ヤング係数 E を用いて d²y/dx² = -M/EI と表されます。㋐ は「-M(x)」です。正解は 1 ~ 3 です。

㋑ ですが
考慮すべき条件は y'(0) = 0 です。正解は 1 or 2 です。

㋒ ですが
片持ち梁、等分布荷重における先端部分のたわみなので「wl⁴/8EI」です。これは公式として記憶していることが期待されます。

以上より、正解は 2 です。

類題 H26 no22
https://yaku-tik.com/koumuin/h26-doboku-22/