公務員試験 2021年 国家一般職(土木) No.21 解説

　問 題　　　　　

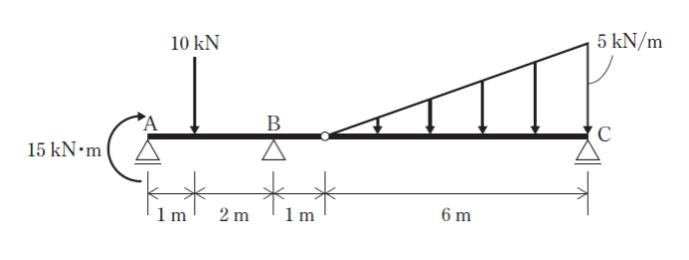
図のように、曲げモーメント、鉛直集中荷重及び等変分布荷重が作用するゲルバー梁の支点A における鉛直反力の大きさはいくらか。ただし、梁の自重は無視するものとする。

1． 0 kN
2． 5 kN
3． 10 kN
4． 15 kN
5． 20 kN

 

 

 

 

 

　解 説　　　　　

ゲルバー梁の定石「ピン部分で分ける」で考えます。ピン部分を d とします。まず d よりも右側に注目します。等変分布荷重部分は集中荷重に直します。三角形の面積である 15 kN の集中荷重です。作用するのは重心部分なので、右端から 2m の点になります。

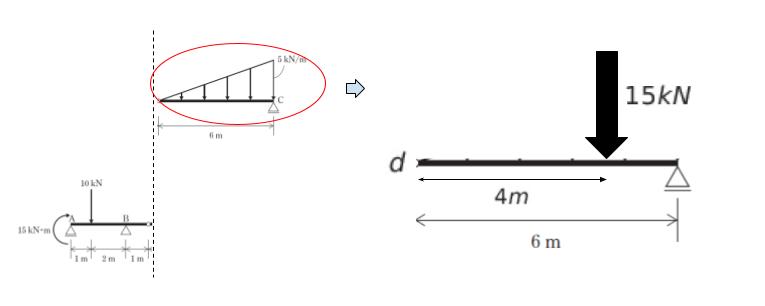
ピン部分なので、点 d 周りのモーメントの和が 0 です。

点 C における縦方向 上向きの反力を Rc とおけば、Rc によるモーメントが Rc × 6 (反時計回り) です。15kN によるモーメントが 15 × 4 = 60 kN・ｍ(時計回り) です。従って、Rc = 10 とわかります。

縦方向の力の和が 0 なので、点 d において 上向きに 15 – 10 = 5 kN のせん断応力 Qd が作用することがわかります。これにより、ピン部分で分けた左部分に注目した際、d には せん断応力が下向きに 5kN の力が作用します。

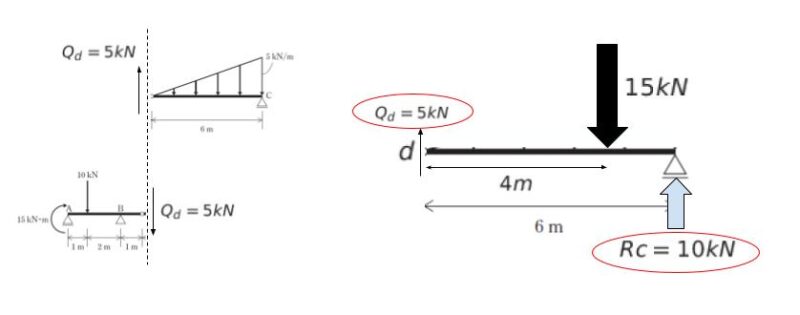
ピン部分で分けて d 部分よりも左側に注目します。
上向きの支点反力 R_A、R_B と仮定します。

・縦方向の力の和が 0 なので
R_A + R_B = 15…(1)

点 d 周りのモーメントに注目すれば
・R_B によるモーメント：R_B × 1 = R_B (時計回り)
・R_A によるモーメント：R_A × 4 = 4R_A (時計回り)
・15kN・m の曲げモーメント (時計回り)

・下向き 10 kN によるモーメント：10 × 3 = 30 (反時計周り)

なので、4R_A + R_B = 15…(2) です。

(1),(2) を連立すれば、R_A = 0 です。ちなみに、R_B = 15 とわかります。

以上より、正解は 1 です。