問 題
確率変数 X の確率密度関数 f(x) が、定数 k を用いて
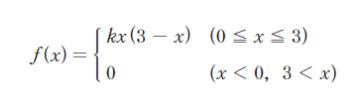
と表されるとき、k の値はいくらか。
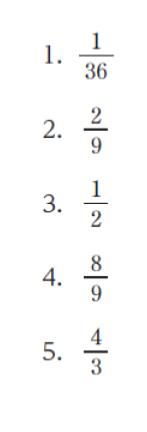
正解 (2)
解 説
【確率密度関数の基礎知識】
確率といえばサイコロなどが代表的ですが、取りうる値が 1,2,3,4,5,6 のように「とびとび」ではなく 1 ~ 6 まで、例えば 1.2, 4.5 といった「連続する値のうちの何か」が結果として出る場合もあります。このような場合において、ある値の出やすさを表すのが「確率密度関数」です。※ 確率密度関数の特徴:全範囲を積分すると 1
確率密度関数の特徴から
0 ~ 3 まで kx(3 – x) を積分すると 1 です。本問と同年度 2021 年の no4 にあったように
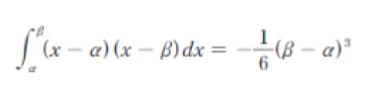
なので
-k ∫(x-0)(x-3) とみれば、k を除いた部分である –∫(x-0)(x-3) は α = 0、β = 3 より、33/6 = 27/6 = 9/2 です。
従って
-k ∫(x-0)(x-3) = 9k/2…(1) です。
確率密度関数では (1) = 1 です。
k = 2/9 とわかります。
以上より、正解は 2 です。

コメント