問 題
2 次方程式 x2 -(3a – 1)x – a = 0 の二つの解が sinθ、cosθ (0 ≦ θ < 2π) であるとき、正の定数 a の値はいくらか。
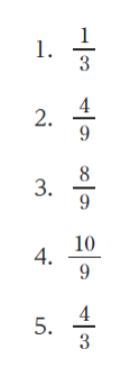
正解 (2)
解 説
選択肢 から a の候補は 5 つなので、a を代入すれば単なる二次方程式で答えがでます。しかし「それが sinθ、cosθ といえるのか?」という点の確認が大変で、具体的に考えてもうまくいかなそうな問題です。別方針を考えます。
解が sinθ、cosθ であることから、方程式の左辺は (x – sinθ)(x – cosθ) と因数分解できます。展開して、元の方程式の左辺と係数を比較すれば
・3a – 1 = sinθ + cosθ…(1)
・-a = sinθ cosθ…(2) です。
※「解と係数の関係」を覚えていれば
そこからいきなり式 (1),(2) を見つけても OK
sinθ と cosθ なので
「sin2θ + cos2θ = 1」…(3) でなければいけません。
sin2θ + cos2θ = (sinθ + cosθ)2 – 2sinθcosθ と変形すれば、(1),(2) より (3) を (3a – 1)2 -2 × (-a) = 1…(3)’ という 「a の 2 次式」に直せます。選択肢 の a の値を代入していけば、a = 4/9 の時に (3)’ が成立します。
以上より、正解は 2 です。

コメント