問 題
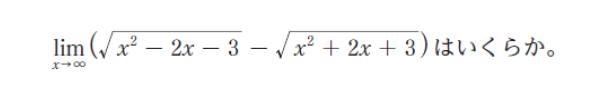
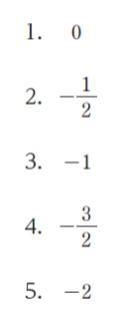
正解 (5)
解 説
x → ∞ の時 x2 – 2x -3 も x2 + 2x + 3 も ∞ になるため「∞ー∞」の形です。√ が含まれる、不定形の極限ときたら「有理化」が定石です。知らなかった人は本問でぜひ見慣れておきましょう!分母は 1 とみなし、√ を外すため分母・分子に √x2 – 2x – 3 + √x2 + 2x + 3 をかけます。
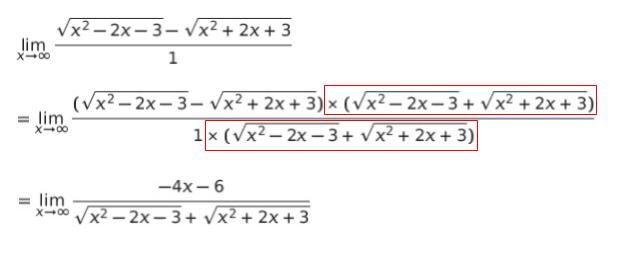
今度は ∞/∞ の形です。この形では「分母の最高次数で、分母・分子を割る」が定石です。これにより「1/x や 1/x2」といった、x → ∞ で 0 になる形を作る意図の変形です。分母の最高次は「√x2」なので、分母・分子を「x」で割ります。
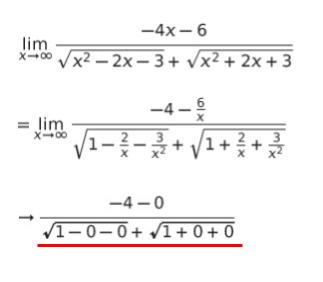
これで分母は 1+1、分子は -4 となので、-4/2 = -2 です。
以上より、正解は 5 です。

コメント