問 題
AB = 7、BC = 5,CA = 6 である △ABC の内接円の半径はいくらか。
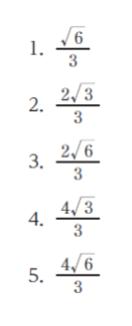
解 説
【三角形の内接円に関する基礎知識】
三辺の長さ a,b,c の三角形があり、面積を S とします。この時、内接円の半径を r とすれば、以下のような関係が成り立ちます。「三辺の長さ」、「面積」、「内接円の半径」の3つのうち2つがわかれば、後1つも計算できるという関係です。
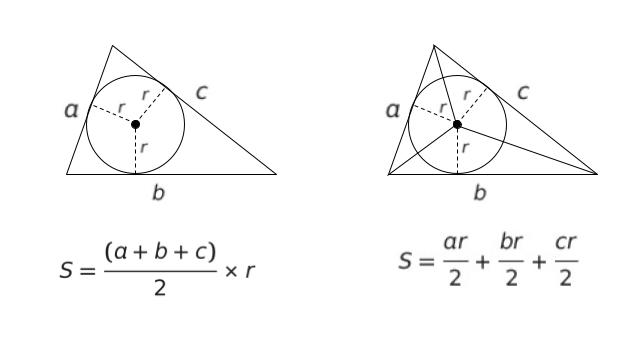
【解法 1:ヘロンの公式 or S = absinθ/2 で面積を出す】
内接円の面積を出すために、三辺の長さがわかっているため後は「面積」が必要です。三辺の長さ → 面積 は「ヘロンの公式」で求めることができます。「三辺の和の半分を s」とおくと、面積 S = √s(s-a)(s-b)(s-c) です。
s = 9 なので、S = √9×4×3×2 = √216 = 6√6 です。
また三辺の長さ → cos θ を余弦定理で求めることができます。cos θ = (a2+b2-c2)/2ab なので、a = 5,b = 6,c = 7 とすれば、cos θ = 12/60 = 1/5 です。cos θ がわかると sin θ もわかります。sin2θ + cos2θ = 1 より、sinθ = 2√6/5 です。
従って、底辺 5、高さ 12√6/5 より 面積が 6√6 とわかります。※ S = absinθ/2 という公式に代入しても OK です。
面積 6√6 を得れば、S = (a+b+c)/2 × r より
6√6 = 9 × r
∴r = 2√6/3
以上より、正解は 1 です。
【解法 2:具体的に考える、近似して正三角形とみなす】
7,6,5 の三角形は近似して「1辺 6 の正三角形」とみなします。面積は 正三角形の面積の公式:S = √3a2/4 より 9√3 です。従って、内接円の半径は √3 ≒ 1.7 です。1.7 に近い選択肢を選べば、選択肢 3 となります。
※選択肢を 小数第 1 位で近似すれば、√3 ≒ 1.73、√6 ≒ 2.45 より
選択肢 1:√6/3 ≒ 2.45/3 ≒ 0.8
選択肢 2:2√3/3 ≒ 3.46/3 ≒ 1.1
選択肢 3:2√6/3 ≒ 選択肢 1 × 2 ≒ 1.6
選択肢 4:4√3/3 ≒ 選択肢 2 × 2 ≒ 2.2
選択肢 5:4√6/3 ≒ 選択肢 3 × 2 ≒ 3.2
以上より、正解は 3 です。

コメント