2021年国家一般職(電気・電子・情報) No.33解説

　問題　　　　　

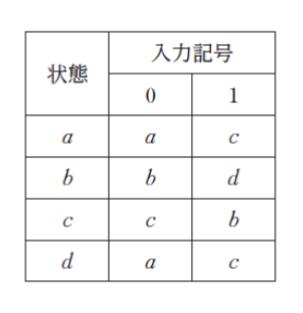
表は、入力記号の集合が {0、1}、状態集合が {a、b、c、d} である有限オートマトンの状態遷移表である。初期状態を a、受理状態を d とするとき、次の㋐～㋔の記号列のうち、この有限オートマトンで受理される記号列のみを全て挙げているのはどれか。

㋐ 001011
㋑ 010110
㋒ 011111
㋓ 101001
㋔ 110111

1．㋐、㋒
2．㋐、㋓
3．㋐、㋔
4．㋑、㋒
5．㋒、㋓、㋔

正解 (2)

　解説　　　　　

表の読み方は「状態が a だったら、入力 0 の場合状態 a のまま、入力 1 だったら c になってください」といったものです。各状態と入力に応じた変化が示されています。

有限オートマトンでは「入力が終了した時に受理状態　であれば『OK,受理しよう』という判断をする」というのが前提知識となります。すると、入力の本当に最後の 1 個は「受理状態である d に遷移する入力」でなければいけません。表を見てみると d に遷移しうるのは 1 のみです。

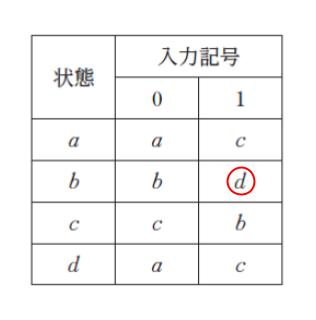
従って
最後が 0 である㋑は誤りです。選択肢 4 は誤りです。

㋐ですが
初期状態が a で記号列が 001011 なので aaccbd と状態が変化します。最後が受理状態の d なので、この記号列は受理されます。㋐は妥当です。正解は 1,2,3 のどれかです。

㋒ですが
初期状態が a で記号列が 011111 なので acbdcb と状態が変化します。最後が受理状態の d ではないので、この記号列は受理されません。㋒は妥当ではありません。選択肢 1 は誤りです。

㋓ですが
初期状態が a で記号列が 101001 なので ccbbbd と状態が変化します。最後が受理状態の d なので、この記号列は受理されます。㋓は妥当です。

以上より、正解は 2 です。

コメント