問 題
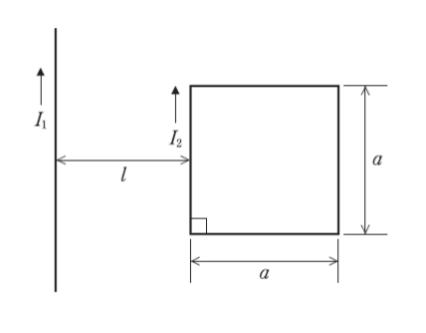
図のように、真空中に、無限に長い導線と、導線から距離 l だけ離れた一辺の長さが a の正方形の回路がある。図の矢印の向きに、導線に大きさ I1、正方形の回路に大きさ I2 の電流を流したとき、導線と正方形の回路間に作用する力として最も妥当なのはどれか。
ただし、真空中の透磁率を μ0 とし、導線と正方形の回路は同一平面上にあり、正方形の各辺は導線と平行又は垂直であるものとする。また、導線と回路導体の太さは無視できるものとする。
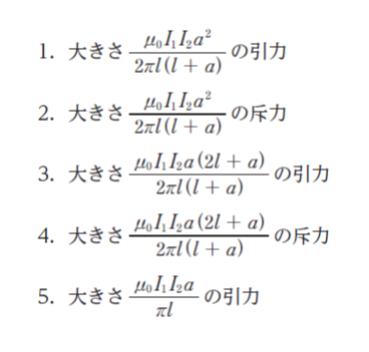
解 説
【電磁力に関する基礎知識】
I(A) の電流が流れる長さ l (m) の導体と、磁束密度 B (T) の一様な磁界が直行する時、大きさ IBl の力が作用します。
向きはフレミングの左手の法則に従います。親指、人差し指、中指をそれぞれ直角に開き、中指を電流の向き、人差し指を磁界の向き (棒磁石であれば N → S) とすると、親指が力の向きと対応します。
正方形の導線は、直線導線 4 つに分けて考えます。
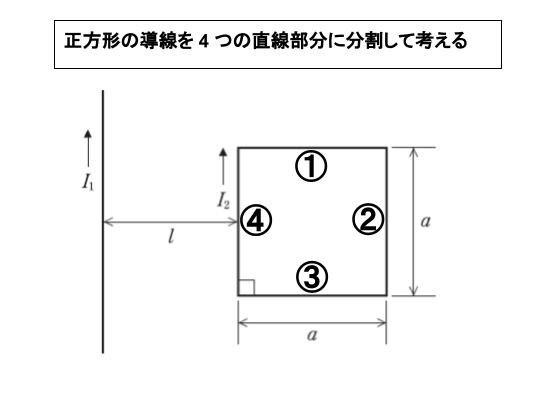
左側の無限に長い直線電流により磁界が生じます。十分長い直線電流 I が作る磁場の強さ H は、直線から r 離れている場所において H = I/2πr…(1) です。磁界の向きは「紙面表から裏に突き抜ける方向」です。電流と磁界が直行するので、① ~ ④ に IBl の力が発生します。
① と ③ については、電流の向きだけ逆になるので、力が打ち消し合って 0 です。そのため無視してかまいません。
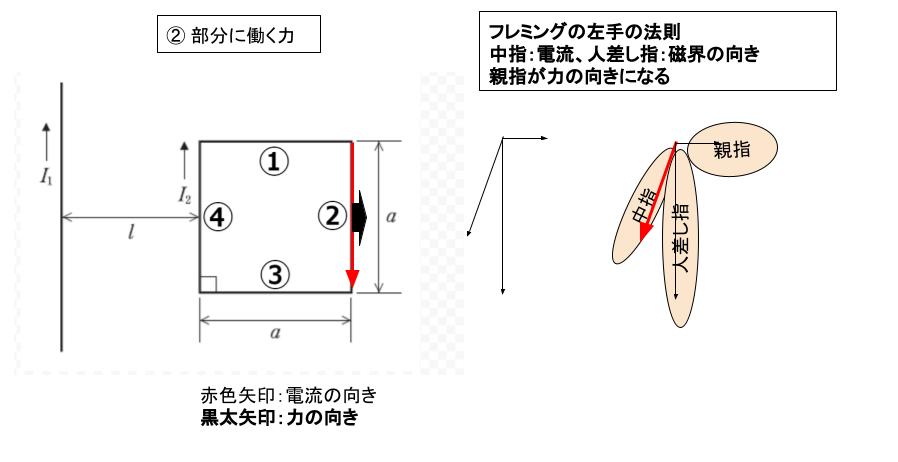
② について
無限に長い直線導線からの距離が (l + a) です。 力の向きがフレミングの左手の法則より、直線導線から離れる向きになります。
④ について
無限に長い直線導線からの距離が l です。 力の向きがフレミングの左手の法則より、直線導線に近づく向きになります。左手の向きを合わせるのが大変だったら、電流の向きだけが逆だから ② と逆方向と考えてもよいです。
② よりも ④ の部分の方が、直線導線に近いため、式 (1) から磁界が大きくなります。その結果、受ける力も大きくなります。
以上をまとめると
「①、③ は無視できて、② と ④ が向きが逆だが 大きさが ④ の方が大きい」です。すると、正方形導線の受ける力の向きは、結局 ④ 部分が受ける力の向きです。つまり「直線導線に近づく方向」に力が作用します。従って「引力」です。正解は 1 or 3 or 5 です。
力の大きさは
「④ 部分が受ける力の大きさ:F④」と、「② 部分が受ける力の大きさ:F②」の差です。
F④ = I2 × (μI1/2πl) × a
F② =I2 × (μI1/2π(l+a)) × a と表せます。差は I2 × μI1 a2/2πl(l+a) です。 差の計算過程は、以下の通りです。※μ0 の 0 は省略しています。
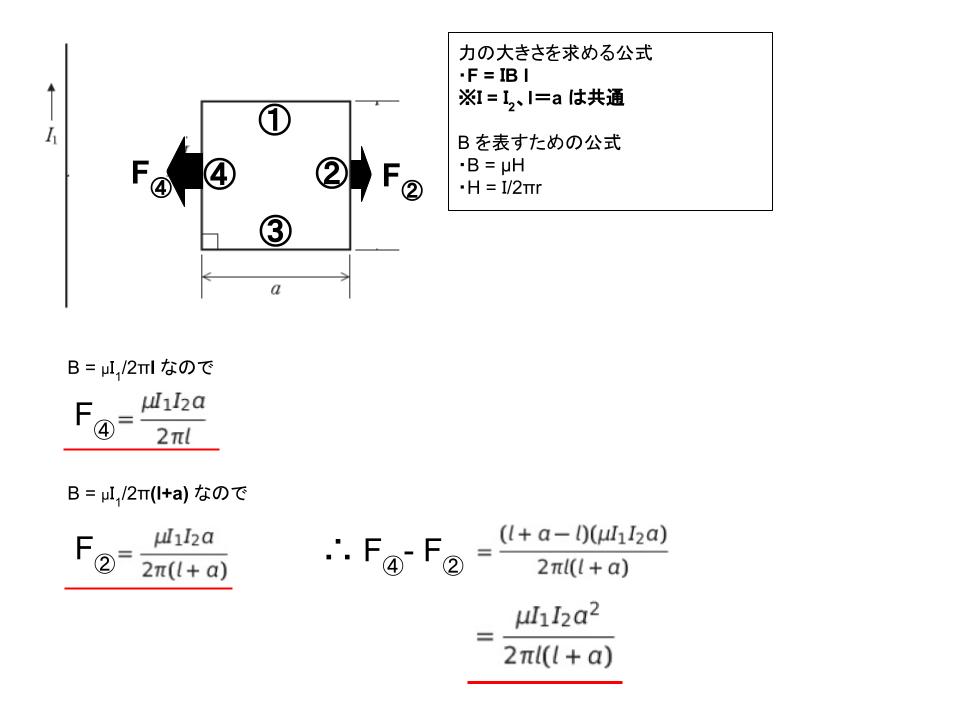
以上より、正解は 1 です。

コメント