問 題
1 ~ 9 の互いに異なる数字が一つずつ表面のみに書かれた 9 枚のカードがある。これらのカードが裏面を上にして置かれており,そのうち 2 枚のカードをめくったところ,書かれていた数字は 4 と 7 であった。その後,残り 7 枚のカードのうち 3 枚をめくったとき,それらの 3 枚のカードに書かれている数字の積が偶数になる確率はいくらか。
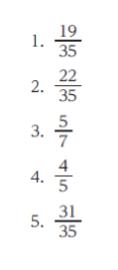
正解 (5)
解 説
1~9 のうち、4 と 7 以外なので
1,2,3,5,6,8,9 の7枚から 3枚を選ぶことになります。
1,3,5,9 が奇数、2,6,8 が偶数です。
3枚の数字の積が偶数である とは、1 枚でも偶数が含まれればよい、ということです。
そこで逆に、積が奇数になる確率を求めます。そして、求めた確率を1から引けば、求めたい「数字の積が偶数になる確率」がわかります。このような考え方を、余事象を用いた解き方といいます。
初めにめくった数が奇数である確率は 4/7 です。
次にめくった数が奇数である確率は 3/6 です。
3番目にめくった数が奇数である確率は 2/5 です。
従って
3枚とも奇数が出て、積が奇数となる確率は
4/7 × 3/6 × 2/5 = 4/35
1-4/35 = 31/35 です。
以上より、正解は 5 です。

コメント