問 題
次の四つの行列がある。
A: 3 行 2 列、B: 2 行 5 列、C: 5 行 1 列、D: 1 行 3 列
これらの積 ABCD を計算するとき、行列成分の乗算の回数が最小となる計算順序として正しいのはどれか。
1.(A (BC) ) D
2.A ( (BC) D )
3.A (B (CD) )
4.(AB) (CD)
5.( (AB) C ) D
正解 (1)
解 説
選択肢 1,2 は、まず BC
選択肢 3,4 は、まず CD
選択肢 5 は、まず AB を計算しています。
一例として
「全成分が 1 である行列」を具体的に考えるとわかりやすいです。
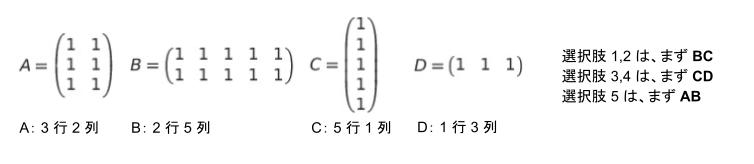
まず BC を計算すると
10 回の掛け算で 「2 行 1 列」の行列ができます。
まず CD を計算すると
15 回の掛け算で 「5 行 3 列」の行列ができます。
まず AB を計算すると
15 回の掛け算で 「3 行 5 列」の行列ができます。
BC の方が掛け算の回数が少ない上に、できる行列も小さくて後の計算が少なくてすみそうです。選択肢 1,2 のどちらかが答えと考えられます。
選択肢 1,2 のうちどちらがより掛け算の回数が少ないか考えます。選択肢 1 は次に A との積、選択肢 2 は次に D との積を計算しています。
A (BC):6 回の掛け算で「3 行 1 列」になります。
(BC)D:6 回の掛け算で「2 行 3 列」になります。
A (BC) の方ができる行列は小さくなります。従って、選択肢 1 の方が、行列成分の乗算の回数が少ないと考えられます。
※最後まで具体的に考えてもかまいません。また、選択肢 3,4,5 についても、具体的に最後まで乗算回数を評価してもよいです。
以上より、正解は 1 です。

コメント