2020 (R2) 年 国税専門官 No.61 解説

　問 題　　　　　

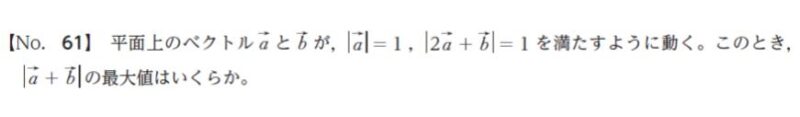
1． 0
2． 1
3． 2
4． 3
5． 4

 

 

 

 

 

　解 説　　　　　

|a| = 1、|b| = 1 の時に |a + b| の最大値であれば簡単なのですが、少しひねりのあるベクトルの問題になっています。初見で数分間で解くのは少し難しい印象です。

簡単な問題の形に合わせるために u = a、v = 2a + b とおきます。すると a + b を以下のように u,v を使って表せます。

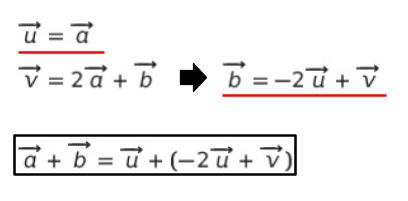
整理すれば
|u| = 1,|v| = 1 の時 |－u + v| の最大値を求めればよい問題になります。

u,v は 共に絶対値が 1 なので、図形的には「原点中心、半径 1 の円上の点」と「原点」を結んだ矢印ベクトルです。

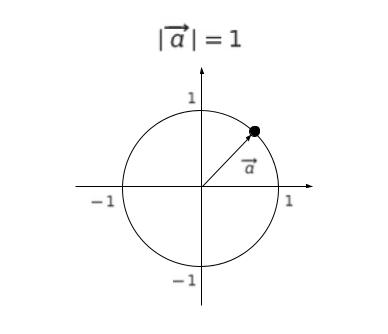
従って、図形的に考えれば |－u + v| の最大値 はすぐに 2 とわかるかもしれません。

図形的にピンとこなければ、ベクトルの定石である絶対値の 2 乗で計算すればよいです。|-u + v| = k とおき、両辺を 2 乗します。

|u|² = |v|² = 1 より -2 u・v の範囲が問題となります。u・v = |u||v|cosθ より u・v = cos θ です。-1 ≦ cos θ ≦ 1 です。これは三角関数の基礎知識です。

従って
k² の最大値が 1 + 1 + 2 = 4 です。
→ k の最大値は 2 とわかります。※「選択肢は 3」となる点に注意！ 

以上より、正解は 3 です。