問 題

A~Jの10 人は,将棋のトーナメント戦を行った。トーナメントの形式は図のとおりであり,空欄にはG~Jのいずれかが入る。次のことが分かっているとき,確実にいえるのはどれか。
○ ちょうど 2 勝したのは 3 人であった。
○ BとIは準決勝で対戦し,その勝者は優勝した。
○ Fは,EともJとも対戦しなかった。
○ GとHはそれぞれ 1 試合目で負けたが,H はその試合で勝っていたら次は準決勝であった。
1.ちょうど1 勝したのは 1 人であった。
2.GはCに負けた。
3.Fは準優勝であった。
4.IはDと対戦した。
5.Jは 1 試合目で勝った。
解 説
トーナメントでは、1試合で1人勝ち、1人負けます。1人が勝ち残るまで試合が行われるため、「登場人物-1」が総試合数です。これはトーナメントの基礎知識です。本問では10人いて、残りが1人になるまでに 10 ー 1 = 9 試合行われ、計9勝 です。
条件「ちょうど2勝が3人」より、残りの勝利数は 9-2×3=3勝です。2勝では優勝できないトーナメント表なので、3勝が1人います。そして、他に勝った人はいません。この時点で選択肢 1 は誤りです。
B と I が準決勝で対戦なので、I は C の隣と確定します。B がもし優勝したとすると、4勝になってしまうため、B と I の準決勝における勝者は I です。トーナメント表左半分の勝ち負けが以下のようになります。
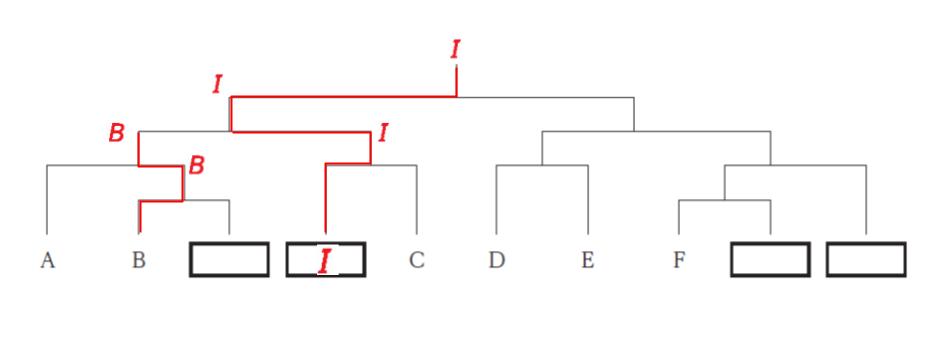
条件 「H は1試合目で負けたが、勝っていれば次が準決勝」より、 H は右端です。そして、F の対戦相手としては 残っている G or J ですが、条件「F は E とも J とも対戦しなかった」とあるため、F の相手が G です。残っている B の1回戦の相手が J です。以下のように確定します。

空欄を埋めることができたので、選択肢を検討してみます。明らかに 選択肢 2,5 は誤りです。正解は 3 or 4 です。そして、F はちょうど2勝なので、準優勝ではありません。選択肢 3 も誤りです。
以上より、正解は 4 です。
トーナメントの勝敗を確定させると、以下のようになります。


コメント