公務員試験 2020年 国家一般職(土木) No.30解説

　問 題　　　　　

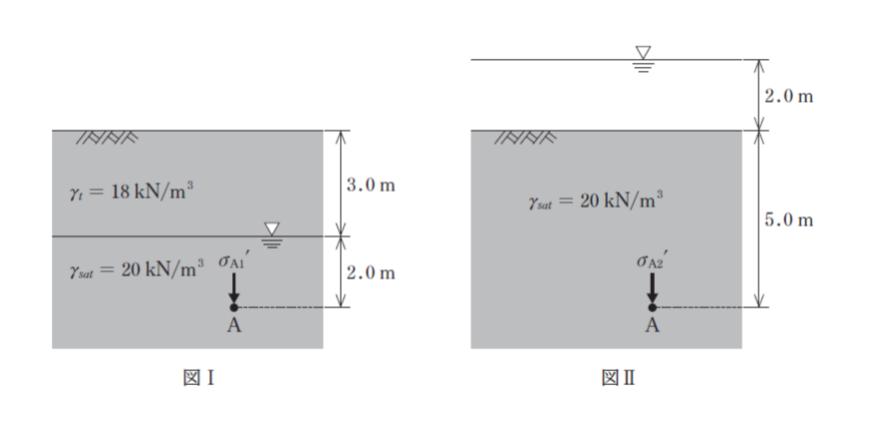
図Ⅰのように地表面から深さ 3.0 m の位置に地下水面があり、地表面から深さ 5.0 m の点 A に鉛直有効応力 σ_A1‘ が作用している。いま、その状態から水位が変化して図Ⅱのように地表面から高さ 2.0 m の位置まで水面が上昇し、Aに作用する鉛直有効応力は σ_A2‘ となった。このときの σ_A1‘ から σ_A2‘ への変化として最も妥当なのはどれか。

ただし、水面より下の土は飽和しているものとし、土の飽和単位体積重量 γ_sat 及び湿潤単位体積重量 γ_t をそれぞれ 20 kN/m³、18 kN/m³、水の単位体積重量を 10 kN/m³ とする。

1．およそ 0.68 倍に減少
2．およそ 0.95 倍に減少
3．変化なし
4．およそ 1.1 倍に増加
5．およそ 1.3 倍に増加

 

 

 

 

 

　解 説　　　　　

水がある所は浮力がかかるため、単位体積重量を、水の分だけ軽く考えるのがポイントです。

図Ⅰについてですが
水位より上なら 1 m あたり 18 kN/m²、水位より下なら 1 m あたり 浮力受けて 20 – 10 = 10 kN/m² ということです。従って、σ_A1‘ = 18 × 3 + 10 × 2 = 74 kN/m² です。

図Ⅱについてですが
σ_A2‘ = 20 – 10 = 10 × 5 = 50 kN/m² です。水が上に乗っていますが、本問で聞かれているのは「有効応力」なので、上に乗っている水は無視して大丈夫です。

σ_A1‘ 74 → σ_A2‘ 50 なので
選択肢を参考にすれば「およそ 0.68 倍に減少」が妥当です。

以上より、正解は 1 です。

【全応力、有効応力、間隙水圧について】
ちなみにですが
「全応力」が問われる場合は水の重さを加えます。また、その際は浮力を引かないで計算します。

例えば本問の図Ⅱにおいて、全応力は 20 × 5 + 10 × 2 = 120 となる、ということです。全応力と有効応力 (土粒子の骨格に作用する応力) の差である「120 – 50 = 70」は「間隙水圧」を表します。全応力 σ＝ 有効応力 σ’ + 間隙水圧 u が成り立ちます。