問 題
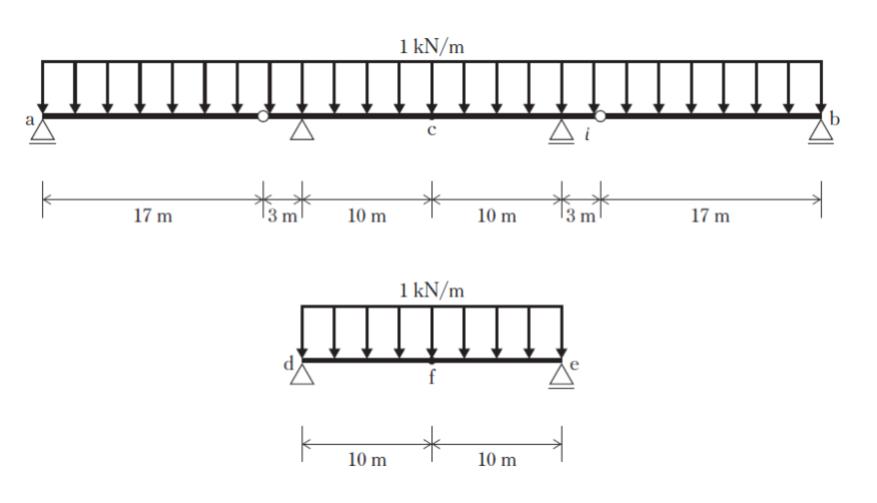
図のように、ab 間に1 kN/m の等分布荷重が作用しているゲルバー梁中央の点 c における曲げモーメントを Mc とする。また、de 間に1 kN/m の等分布荷重が作用している単純梁中央の点 f における曲げモーメントを Mf とする。このとき、 Mc/Mf として最も妥当なのはどれか。ただし、梁の自重は無視できるものとする。
解 説
・簡単な Mf から求めます。
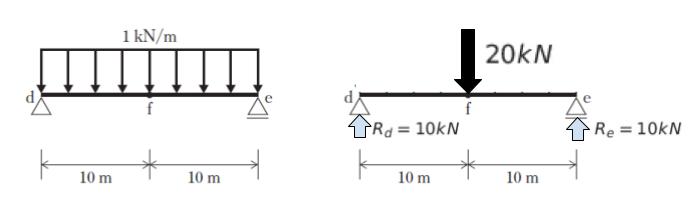
まず反力を計算します。等分布荷重は集中荷重に直します。1kN/m が 20m なので、集中荷重 20kN が ちょうど真ん中に作用します。反力は、対称性から Rd = Re = 10kN です。
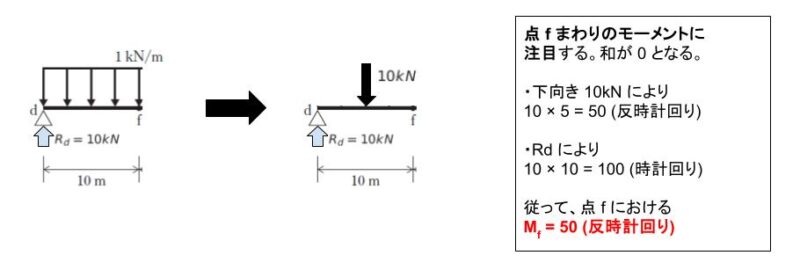
Mf を求めるため、点 f で仮想切断すれば、Mf = 50 (kN・m) とわかります。
・Mc を求めるために、ゲルバー梁の定石「ピン部分で分ける」で考えます。左側のピンを g、右側のピンを h、左側ピン近くの支点を i、右側ピン近くの支点を j とおきます。
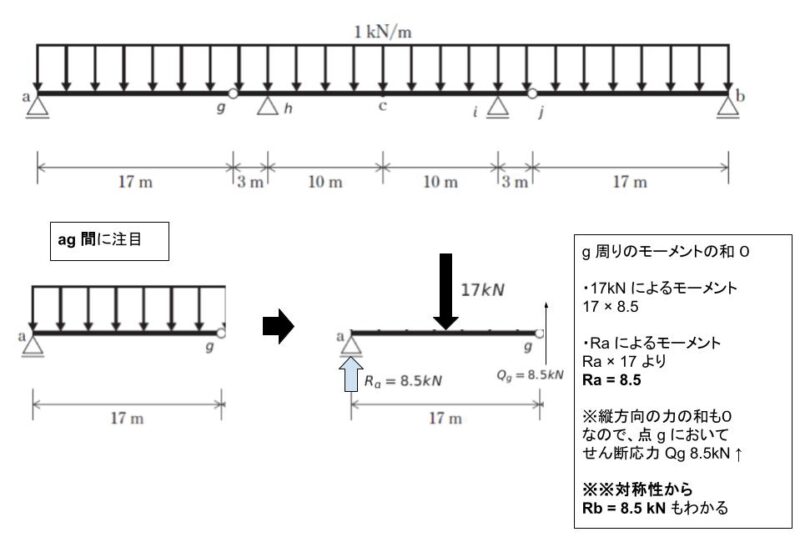
まず ag 間に注目すると、RA = 8.5 です。また g において、上向きに 8.5 kN のせん断応力が作用します。
※g から右側に注目する際には、点 g に下向き 8.5kN のせん断応力が作用することになります。
※※対称性から RB = 8.5 もわかります。
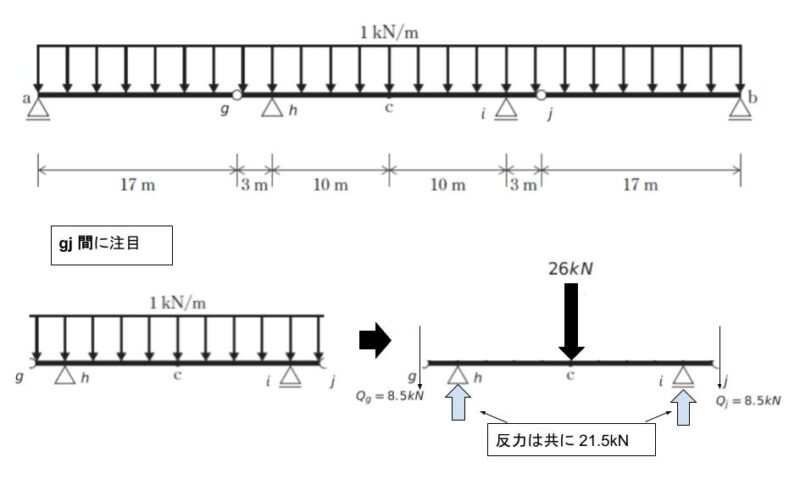
次に 2 つのピンを両端として gj 間に注目します。対称性より j にも下向き 8.5 kN のせん断応力が作用すると考えられます。支点 h,i における反力を Rh、Rj とおきます。対称性から Rh = Rj とします。
等分布荷重を集中荷重に直せば 26kN です。このため、gj 間において下向きに 8.5 + 26 + 8.5 = 43kN 作用しています。半分ずつにすれば Rh = Rj = 21.5kN です。これで全ての反力がわかりました!
・gc 間で仮想切断して、点 c 周りのモーメントに注目します。等分布荷重を集中荷重に直すと 13kN です。モーメントの和は 0 です。
・下向き 13kN によるモーメント:13 × 6.5 = 84.5 KN・m (反時計回り)
・Rh によるモーメント:21.5 × 10 = 215 kN・m (時計回り)
・Qg によるモーメント:8.5 × 13 = 110.5 (反時計回り)
となるため、Mc = 215 – (84.5 + 110.5) = 20 です。
従って
Mc/Mf = 20/50 = 2/5 となります。
以上より、正解は 1 です。

コメント