問 題
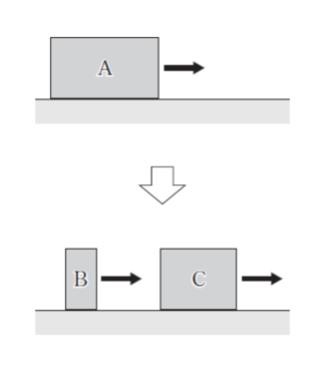
図のように、滑らかな水平面上を速さ V0 で等速直線運動している質量 7 m の小物体 A が、質量 2 m の小物体 B と質量 5 m の小物体 C に瞬間的に分裂した。B と C は、A と同じ方向にそれぞれ等速直線運動をしたが、B は C から見て速さ v で進行方向後方に離れていった。このとき、C の速さとして最も妥当なのはどれか。
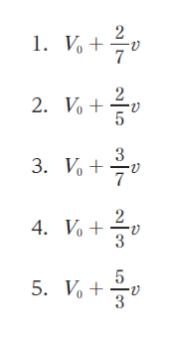
正解 (1)
解 説
運動量保存則から「分裂前後の運動量が保存」されます。
運動量は「質量 × 速さ」です。
・分裂前の運動量:7mV0…(1)
・分裂後の運動量について
選択肢 1 が正解と仮定します。
分裂後の 小物体 C の速さ Vc = V0 + 2v/7 です。
分裂後の 小物体 B の速さ VBは
「C から見て進行方向後方に 速さ v で離れていった」ので
「VB = Vc ー v」です。つまり、V0 – 5v/7 と表されます。
分裂後の運動量は
2m × (V0 – 5v/7) + 5m × (V0 + 2v/7) = 7mV0…(2) です。
(1) = (2) なので
運動量保存則が成り立っています。特に矛盾ありません。
以上より、正解は 1 です。

コメント