問 題
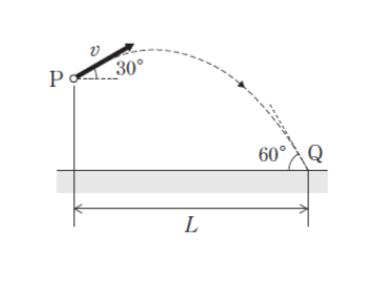
図のように、水平面からある高さの点 P から、小球を速さ v で水平方向と 30° の角度をなすように投げたところ、小球は水平面に対して 60° の角度で水平面上の点 Q に落下した。このとき、P から Q までの水平方向の距離 L として最も妥当なのはどれか。ただし、重力加速度の大きさを g とする。
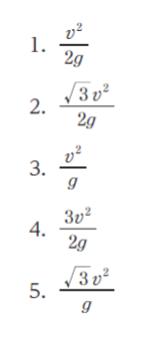
解 説
斜めに玉を投げるのは「斜方投射」です。斜方投射では、垂直方向と水平方向に分けて考えるのが基礎知識です。初速 v を「垂直方向」と「水平方向」に分けるとそれぞれ v/2、√3v/2 です。
点 P から↗️↘️↘️ と小球が動いていきます。
点 P と同じ高さの点を 点 P’ とおきます。
【点 P から 点 P’ までの水平方向距離】
「垂直方向 初速 v/2、重力加速度 g
→ t = v/2g の時に最高点」 ※ これは基礎知識 公式として暗記して OK
→ 2倍した t’ = v/g の時に、点 P と同じ高さである P’ に到達します。
P → P’ 間において水平方向に
初速 √3v/2、t = v/g より √3v2/2g 進みます。
P → Q 間の水平方向の距離 L は明らかに √3v2/2g よりも大きくなります。このため、選択肢 1,2 は誤りです。
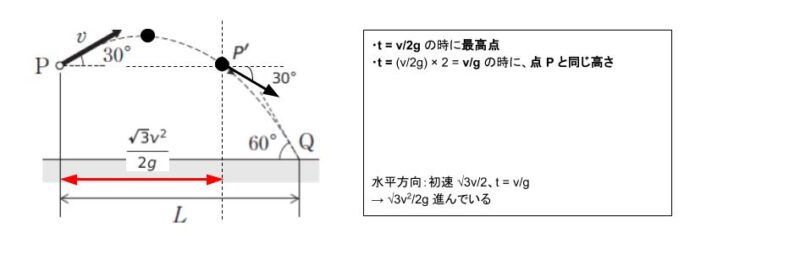
【点 P → 点Q】
点 Q における速度を「垂直方向」と「水平方向」に分けるとそれぞれ 3v/2、√3v/2 です。
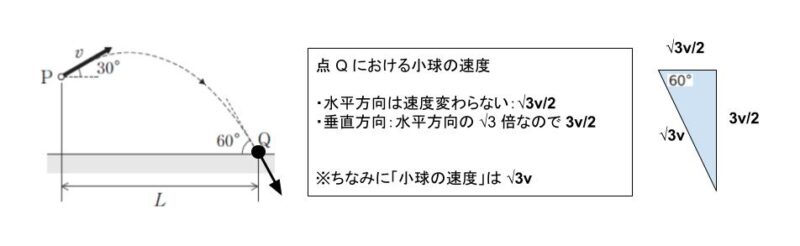
垂直方向に注目します。小球が最高点の時点において垂直方向の速度 0 なので、そこから考えます。最高点を O とします。
O → Q までの垂直方向に注目します。
初速 0、重力加速度 g → gt = 3v/2 になるのは t = 3v/2g の時です。
小球 P を投げた時から最高点に到達するまでの時間 v/2g なので、投げてから 点 Q までにかかる時間は 「P → O」 + 「O → Q」: v/2g + 3v/2g = 2v/g です。
従って、P から Q までの水平方向の距離 L は
L = √3v/2 × 2v/g = √3v2/g
以上より、正解は 5 です。

コメント