公務員試験 2020年 国家一般職(土木) No.6解説

　問 題　　　　　

x > 0、y > 0、log₄y = (log₂x)² であるとき、log₂(x/y) の最大値はいくらか。

 

 

 

 

 

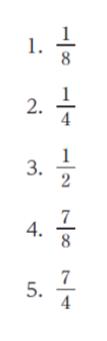
　解 説　　　　　

【解法 1：底の変換公式の活用】
方程式の両辺で底が異なるため、底をまず揃えます。
底の変換公式は以下の通りです。

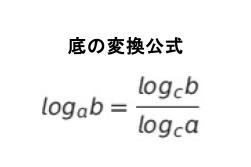
左辺 log₄y = log₂y/log₂4 = log₂y/2 です。

方程式 log₄y = (log₂x)² の両辺に 2 をかければ
log₂y = 2(log₂x)²…(1)　です。

最大値を求めたい log₂(x/y) = log₂x ー log₂y です。(1) より
log₂x ー log₂y
= log₂x ー 2(log₂x)² …(2)　です。

log₂x を X とおけば、(2) は f(X) = X ー 2X² と表せます。この最大値は 微分してもいいし、平方完成して求めてもかまいません。

f(X) = -2X² + X とおきます。
微分するとf'(X) = -4X + 1 となります。
f'(X) = 0 となる時に最大値をとるので、X = 1/4 です。

または平方完成して
f'(X) = -2(X – 1/4)² + 1/8 と変形しても OK です。
やはり X = 1/4 の時最大値 1/8 を得ます。

以上より、正解は 1 です。

【解法 2：具体的に考える】
多くの問題では具体的に考える戦術がおすすめですが、本問は少し難しい印象です

x = 1,y=1 → log₂1/1 = 0
x = 2,y=4 → log₂2/4 = -1

… 選択肢のように正の値にするのすら大変…

x,y をそれぞれ 2^◯、4^△ とおきます。方程式から △ = ◯² …(1) です。

x/y = 2^◯/4^△
=2^◯/2^2×△
=2^(◯ー2△) です。

従って、log₂x/y の最大値を求めるには
◯ー2△ の最大値を考えればよいです。

さらに (1) より
◯ー2◯² の最大値を求める問題に帰着します。

f(◯) = -2◯² + ◯ とおきます。
微分するとf'(◯) = -4◯ + 1 となります。
f'(◯) = 0 となる時に最大値をとるので、◯ = 1/4 です。

または平方完成して
f'(◯) = -2(◯ – 1/4)² + 1/8 と変形しても OK です。
やはり ◯ = 1/4 の時最大値 1/8 を得ます。

以上より、正解は 1 です。