問 題
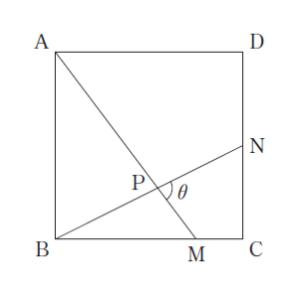
図のように、正方形 ABCD において、辺 BC を 3:1 に内分する点を M、辺 CD の中点を N、線分 AM と線分 BN の交点を P、∠MPN = θ とする。このとき、cos θ はいくらか。
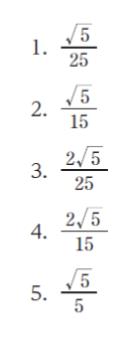
正解 (3)
解 説
都合良い設定として「3 : 1 に内分」する点があるため、1 辺 4 の正方形とします。点 B を原点 (0,0) とすれば、点 A (0,4)、点 C (4,0)、点 M (3,0)、点 N (4,2) です。
cos θ が聞かれているため、ベクトルの内積を考えます。
以下の公式は基礎知識です。

θ は AM と BN がなす角です。ベクトル、大きさ、内積はそれぞれ以下の通りです。従って、cos θ = 2√5/25 です。
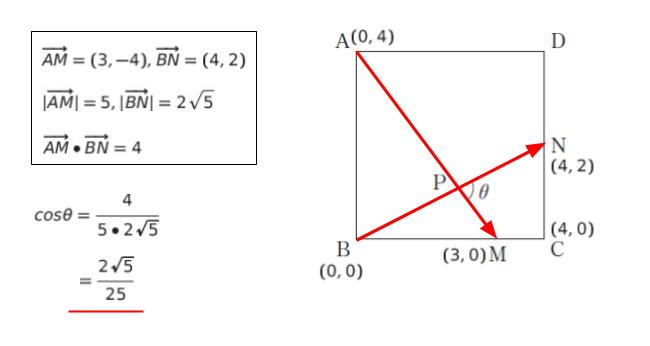
以上より、正解は 3 です。

コメント