問 題

正解 (1)
解 説
y = 1/(x+1) – 1/(x+3) と変形して積分できる人はそれで OK です。積分計算過程の一例は以下の通りです。
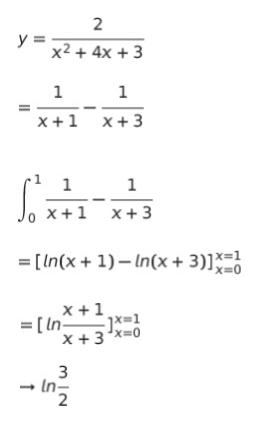
式変形は経験がないと厳しい印象です。浮かばなかった時は「グラフの概形を書き、面積を概算して評価」したい問題です。以降は概算での求め方を解説します。
x = 0 の時 y = 2/3
x = 1 の時 y = 1/4 です。(0,2/3) と (1,1/4) を滑らかにつなぐと、右のように概形を書けます。求めたい面積の概形が左側です。比較のため、縦 1/2,横 1 の長方形を右側に重ねています。
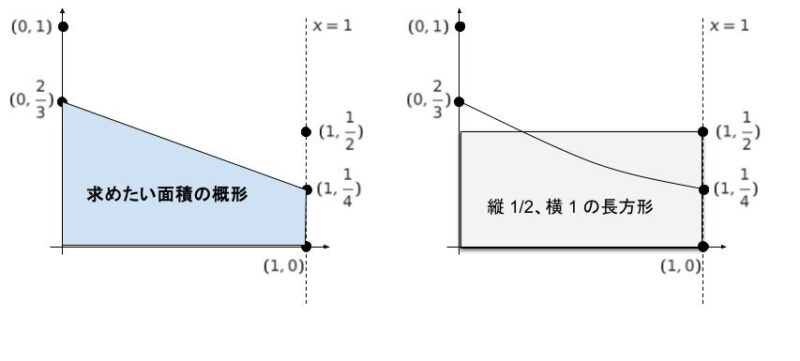
面積 1/2 の長方形と比較すれば、求めたい面積は 1/2 よりやや小さいとわかります。
選択肢を検討します。
e ≒ 2.7 は基礎知識です。2 乗すると 2.7 となる数は 1.6 ~ 1.7 です。つまり e1/2 ≒ 1.6 ~ 1.7 です。
loge 1.7 よりも真数部分が大きい
選択肢 2:loge9/4
選択肢 3:loge8/3 は、1/2 よりも大きい数を表しています。誤りです。
選択肢 5 も 1/2 を超えているため、誤りです。
選択肢 4 ですが
大雑把に見ても、1/2 よりも少ない部分の面積は 1/12 よりは大きそうなので、選択肢 4 は誤りと考えられます。※ 選択肢 1 or 4 で 2 択でも十分と思われます。
以上より、正解は 1 です。

コメント