問 題
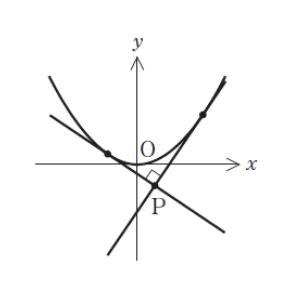

正解 (5)
解 説
接線 を考えるので、微分します。y’ = x…(1) です。
選択肢を見ると、x = 0 の時に -1 or -1/2 をとります。2 本の接線の交点が丁度 y 軸で交わるのは (1,1/2) と (-1,1/2) における接線です。これは図から推測できると思われます。この時、それぞれの接線の傾きは (1) より 1,-1 です。そのため交点は (0,-1/2) とわかります。
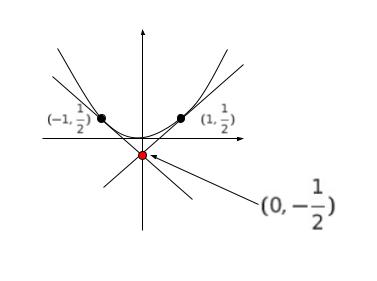
従って、選択肢 1,4 は誤りです。
もう 1 点交点 P を探します。
一例として 点 (2,2) における接線を考えます。傾きは 2 です。
接線が直交するため、もう 1 つの接線の傾きが -1/2 です。そのため、もう 1 つの接点の x 座標は -1/2 です。(-1/2,1/8) と (2,2) における接線を考えます。図に書きこむと大体 y = -1/2 のあたりで交わるので、選択肢 2,3 は誤りと考えられます。
※正確に求めるのであれば
y = 2x – 2 と y = -(1/2)x – 1/8 の交点を求めます。すると交点 P は (3/4,-1/2) です。
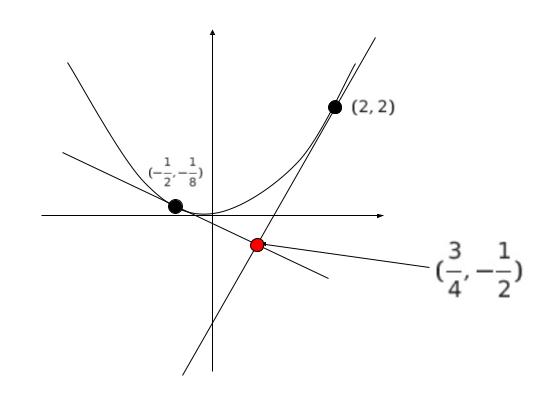
以上より、正解は 5 です。

コメント