問 題
連続な関数 f (x) が区間 [a、b] で常に f(x) ≧ 0 であるとき、曲線 y = f(x) と、x 軸、x = a、x = b で囲まれた図形の面積の近似値 S は次の方法で求められる。
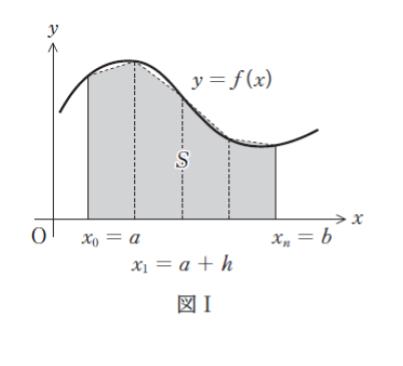
① 図Ⅰのように、区間 [a、b] を n (n > 1) 等分し、刻み幅 h = (b-a)/n とする。各分点の x 座標を x0 = a、x1 = a + h、x2 = a + 2h、…、xn-1 = a + (n – 1) h、xn = b とする。
② 2 直線 x = xi、x = xi+1 と x 軸及び y = f(x) との交点を結んでできる台形の面積を求め、区間 [a、b] におけるこれらの台形の総和を求める。
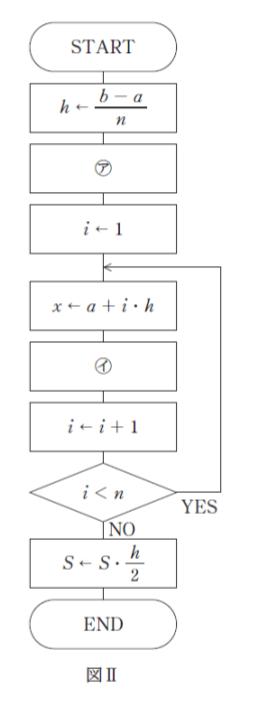
図Ⅱは、この方法をプログラムで実現するときのフローチャートである。図Ⅱ中の ㋐,㋑ に当てはまるものの組合せとして最も妥当なのはどれか。

解 説
具体的に考えるとよいです。また、与えられた図は活用すべきです。例として、図で台形 4 つなので、刻み幅を 1 として「x0 = 1、n = 4、x4 = 5」としてみます。図Ⅰに書き込む形で、以下のようにあらわすことができます。y = f(x) における黒丸の点の座標はそれぞれ、(1,f(x0))、(2,f(x1))、(3,f(x2))、(4,f(x3))、(5,f(x4)) と表せます。
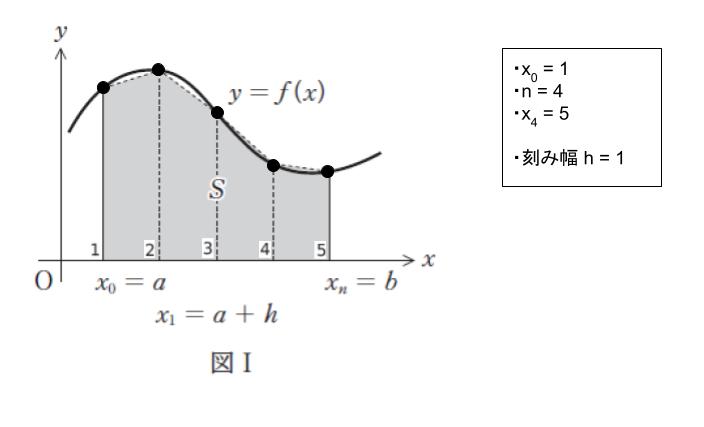
分割された台形の面積について考えます。台形の面積は「(上底 + 下底) × 高さ × 1/2」です。高さが h です。分割された 4 つの台形について、最も左端の台形の上底 は f(x0)、下底 は f(x1) です。そのため、左端の台形の面積は ((f(x0) + f(x1)) × h/2…(1) です。
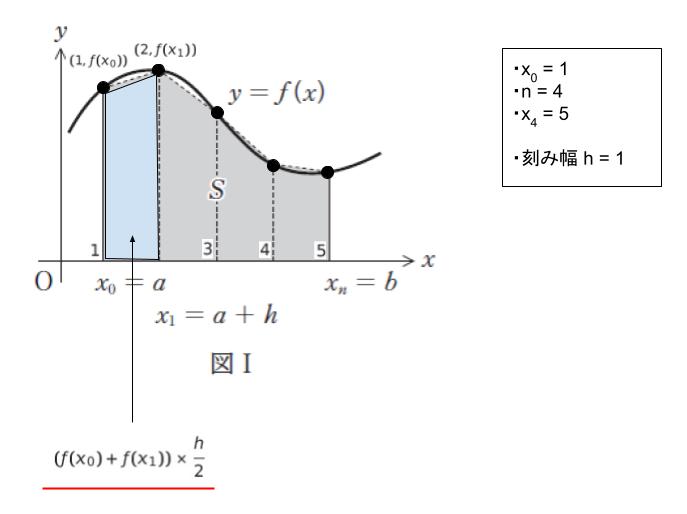
右隣の台形の面積は、同様に考えて (f(x1) + f(x2)) × h/2…(2) です。その右隣の台形の面積は (f(x2) + f(x3)) × h/2)…(3) です。右端の台形の面積は (f(x3) + f(x4)) × h/2…(4) です。(1) ~ (4) を足すことで、面積の近似値が求められます。
ここまでをふまえて、図Ⅱのチャートを見ると、一番最後に「× h/2」をしているので、その前の段階で、例であれば「S = (f(x0) + f(x1)) + (f(x1) + f(x2)) + (f(x2) + f(x3)) + (f(x3) + f(x4))」となっていればよいとわかります。
選択肢を見れば、㋐ は S ← f(a) + f(b) が妥当です。これにより、例であれば f(x0) + f(x4) をまず準備できているということです。残っているのは f(x1)) + (f(x1) + f(x2)) + (f(x2) + f(x3)) + (f(x3) の部分です。
㋑ ですが
S ← S + 2・f(x) が妥当です。この選択肢を入れてチャートを回せば 2・f(x1)、2・f(x2)、2・f(x3) が足されていきます。
以上より、正解は 5 です。
類題 H24 no35 面積の近似
https://yaku-tik.com/koumuin/h24-denjyou-35/

コメント