2020年 国家一般職(電気・電子・情報) No.31解説

　問 題　　　　　

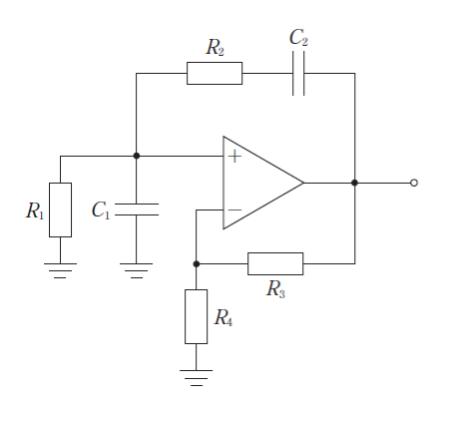
図は演算増幅器を用いたウィーンブリッジ発振回路である。演算増幅器の正相入力端子のところで回路を切り離したと考え、この回路の一巡利得を求めると、

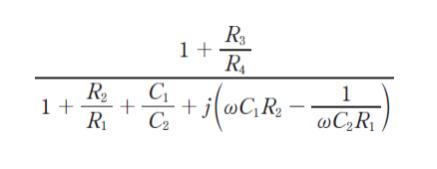
となる。ここで、ω は角周波数、j は虚数単位である。このとき、回路が発振するための振幅条件と、発振周波数の組合せとして最も妥当なのはどれか。ただし、演算増幅器は理想的なものとする。

　

 

 

 

 

 

　解 説　　　　　

発振回路は、自分自身で交流信号を持続的に出力する回路のことです。代表的なものとして、クラップ発振回路、コルピッツ発振回路、本問のウィーンブリッジ発振回路などがあります。発振回路についての知識は本問の解答には不要です。

ーーー
発振周波数は、選択肢の式の形も参考にして「共振条件」と考えます。つまり「複素数 虚数部分 の 係数が 0」になる場合を求めればいいです。

ωC₁R₂ = 1/ωC₂R₁ をとけば、ω =√(1/C₁C₂R₁R₂) です。ω は角振動数なので、周波数 を f = とおけば、2Πf = ω ∴ f = ω/2Π です。 従って、発振周波数は 1/2Π√C₁C₂R₁R₂ です。計算過程は以下のようになります。

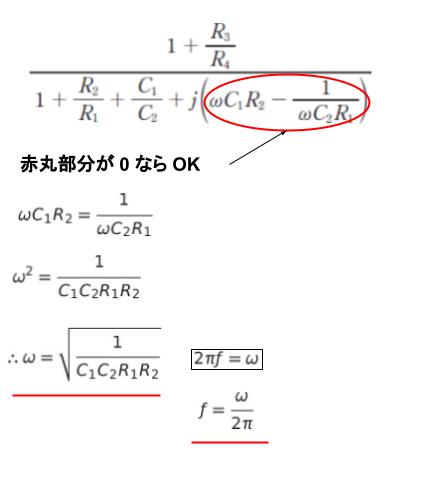
発振周波数 の時に、回路の一巡利得が (1+R₃/R₄)/(1+R₂/R₁ + C₁/C₂)…(1) となります。利得が 1 よりも小さいと「だんだん小さくなる」→ 振幅が 0 になる → 回路が発振しつづけないため、これだとダメ と推測できると思われます。従って、振幅条件は (1) ≧ 1 です。変形すれば、R₃/R₄ ≧ R₂/R₁ + C₁/C₂ です。計算過程は以下の通りです。

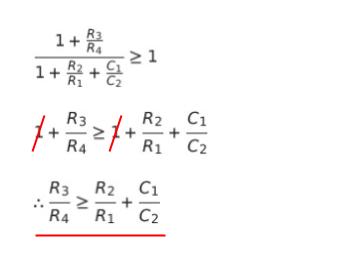
以上より、正解は 1 です。

類題 2019 no31 発振回路
https://yaku-tik.com/koumuin/2019-denjyou-31/