問 題
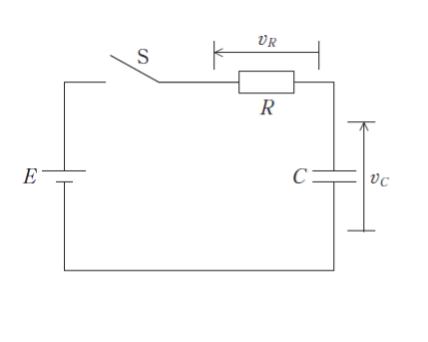
図のような、抵抗値 R の抵抗、静電容量 C のコンデンサ、電圧 E の直流電圧源、スイッチ S からなる回路がある。最初、コンデンサに電荷は蓄えられておらず、S は開いていた。時刻 t = 0 で S を閉じたとき、t における抵抗の両端にかかる電圧 vR と、コンデンサの両端にかかる電圧 vC の組合せとして最も妥当なのはどれか。ただし、e は自然対数の底を表している。
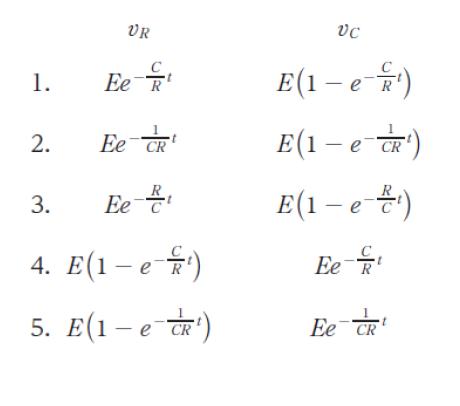
解 説
十分に時間が経つと、コンデンサの両端に+、-の電荷が蓄えられます。この時、コンデンサの極板間には電流が全く流れていないため「抵抗が無限大とみなす」のがポイントです。
すると電流が流れなります。この時、抵抗にかかる VR は 0 です。時間がたつ、つまり t が大きくなった時に VR が 0 になるような選択肢は、e-∞ → 0 より、選択肢 1 ~ 3 です。選択肢 4,5 は誤りです。本問は、ここまで判断できれば十分と思われます。
ここからは具体的数値を使って、イメージで選択肢が絞れればよいです。R がすごく大きいとします。なかなかコンデンサに電荷がたまらないイメージになると思います。すると、t が相当大きくならないと、VR = 0 になりません。
これは e の指数部分における R が 「分母」にあることと対応します。分母にある R が大きいと t が増えてもなかなか 指数部分の数値が大きくならないからです。これにより、R が 指数の分子にある 選択肢 3 が誤りと判断できます。
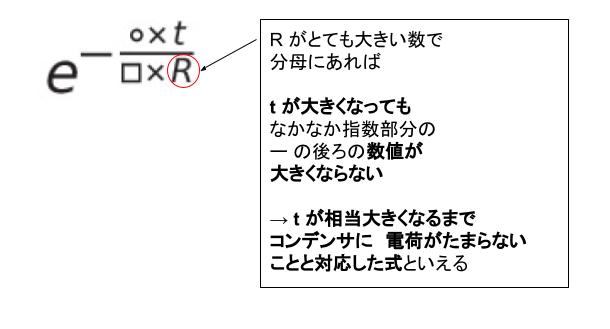
C が大きいと、今度は静電容量が大きいので、やはり電荷がたまるまでに時間がかかるイメージになります。従って、C も指数の分母にあると考えられます。これにより、選択肢 1 が誤りです。
以上より、正解は 2 です。
類題 国家一般職 高卒技術 H27no24
https://yaku-tik.com/koumuin/h27-gijyutu-24/
ーーー以下、完全に補足。公務員試験 技術区分 不要な内容ーーー
ちなみに
キルヒホッフの電圧則から、回路方程式と呼ばれる式を立て、電圧について解けます。
コンデンサに蓄積される電荷 Q = CV…(1) で
i = dQ/dt …(2) なので、(1) 代入して、i = C dV/dt
キルヒホッフの法則より
E – iR – Vc = 0
→ E – CR dV/dt – V = 0 ※Vc を V と書き直しています。
変数分離すれば
dV/dt = (E – V)/CR
dV/(E-V) = dt/CR
辺々 積分して
∫ 1/(E-V) dV = ∫ 1/CR dt
– ln (E-V) = t/CR + A (A は積分定数)
∴ e-t/CR – A = E-V
∴ V = E – e-t/CR – A
※ 但し、t = 0 の時、Vc = 0 より
V = E – e– A × e-t/CR が、t = 0 の時 0 にするため
e– A = E となる A を選ぶ。
→ V = E – E × e-t/CR
→ V = E(1 – e-t/CR)
そして
VR + VC = Eより
VR = Ee-t/CR となります。
公務員試験で 回路方程式を解かないとどうしようもない問題は出題頻度が低く、合格のためには過剰な勉強です。あくまでも参考程度に見てください。

コメント