2020年 国家一般職(電気・電子・情報) No.23解説

　問 題　　　　　

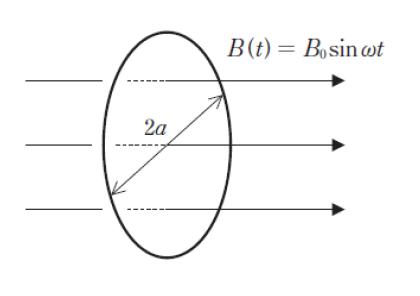
図のように、半径 a、巻数 1 の円形コイルが、時間 t で変化する磁束密度 B(t) = B₀ sin ωt の一様な磁界中に、磁界の向きと垂直に置かれている。ここで、B₀、ω は定数である。このコイルに発生する誘導起電力の最大値 V に関する記述 ㋐ ～ ㋔ のうち妥当なもののみを全て挙げているのはどれか。

㋐　a を 2 倍にしたとき、V は 2 倍になる。
㋑　B₀ を 2 倍にしても、V は変化しない。
㋒　B₀ を 2 倍にしたとき、V は 2 倍になる。
㋓　ω を 2 倍にしても、V は変化しない。
㋔　ω を 2 倍にしたとき、V は 2 倍になる。

 

 

 

 

 

　解 説　　　　　

ファラデーの電磁誘導の法則、V = -N(dΦ/dt) を思い出します。「dΦ/dt」 が、「貫く磁束が時間に対して変化する割合」です。

㋐ ですが
a は半径です。半径が 2 倍になると、円の面積が 4 倍になります。貫く磁束が 4 倍になるので、変化の割合も 4 倍になり、V は 4 倍になると考えられます。「V は 2 倍になる」は誤りです。正解は 4 or 5 です。㋒ は正しいとわかります。

㋓、㋔ ですが
円形コイル内部の面積を S とおけば、Φ = BS です。(sin ωt)’ = ω × cos ωt です。このため、ファラデーの法則の右辺は、dΦ/dt の部分が「ω × ◯」と表せます。つまり、ω に比例します。そのため、ω を 2 倍にすれば、V も 2 倍になります。㋔ が妥当です。

以上より、正解は 5 です。

類題 H24no23
https://yaku-tik.com/koumuin/h24-denjyou-23/