問 題
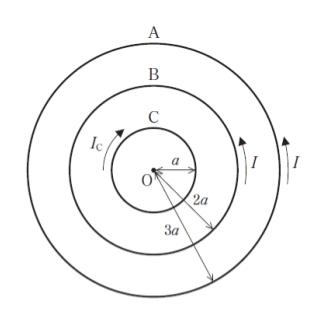
図のように、同一平面上に半径 3a、2a、a の円形導線 A、B、C が、中心 O を共有して配置されている。円形導線 A、B には、それぞれ反時計回りに大きさ I の電流が流れており、円形導線 C には、時計回りに大きさ IC の電流が流れている。中心 O における磁界の大きさが 0 であるとき、IC として最も妥当なのはどれか。
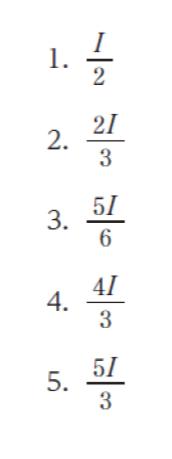
正解 (3)
解 説
【電流と磁場の基本公式】
・無限に長い直線電流 I → 距離 r 離れたら B = μ0I/2Πr
※ アンペールの法則より導出 (本問では使わない)
・半径 r の円形電流 I → 中心の磁束密度 B = μ0I/2r
※ ビオ・サバールの法則より導出 をまず思い出します。
また、B = μH です。H が磁場の大きさです。
ーーー
円形導線 A に流れる電流によって
BA = μ0I/2 × 3a = μ0I/6a
円形導線 B に流れる電流によって
BB = μ0I/2 × 2a = μ0I/4a となります。
円形導線 C に流れる電流によって、BA + BB と同じ大きさの磁束密度となれば、和が 0 になると考えられます。μ0/a は共通なので略すと、BA + BB は (1/6 + 1/4) I = 5I/12…(1) です。
Bc の電流を I’ とおけば
Bc = μ0I’/2a です。μ0/a を略すと Bc = I’/2…(2) です。
従って
I’ = 5I/6 であれば、(1) と (2) が等しくなります。
以上より、正解は 3 です。
類題 H25no22 ビオ・サバールの法則
https://yaku-tik.com/koumuin/h25-denjyou-22/

コメント