2020年 国家一般職(電気・電子・情報) No.21解説

　問 題　　　　　

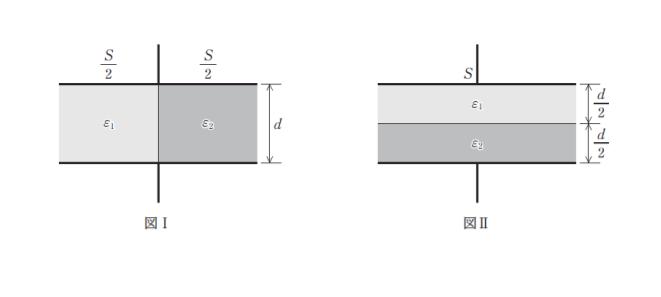
極板面積 S、極板間隔 d の平行平板コンデンサがある。このコンデンサの極板間に、図Ⅰのように、誘電率 ε₁ と ε₂ の誘電体 (それぞれ面積 S/2 、厚さd ) を挿入したときの静電容量 C_Ⅰ と、図Ⅱのように、誘電率 ε₁ と ε₂ の誘電体 (それぞれ面積 S、厚さ d/2 ) を挿入したときの静電容量 C_Ⅱ の組合せとして最も妥当なのはどれか。ただし、端効果は無視できるものとする。

 

 

 

 

 

 

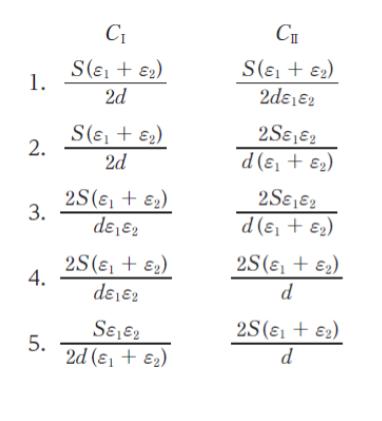
　解 説　　　　　

コンデンサなので、Q = CV、C = εS/d を思い出します。

誘電体の部分的挿入が行われたら、分解して考えます。図Ⅰであれば「並列の２つのコンデンサ」、図Ⅱであれば「直列の 2 つのコンデンサ」と考えれば OK です。

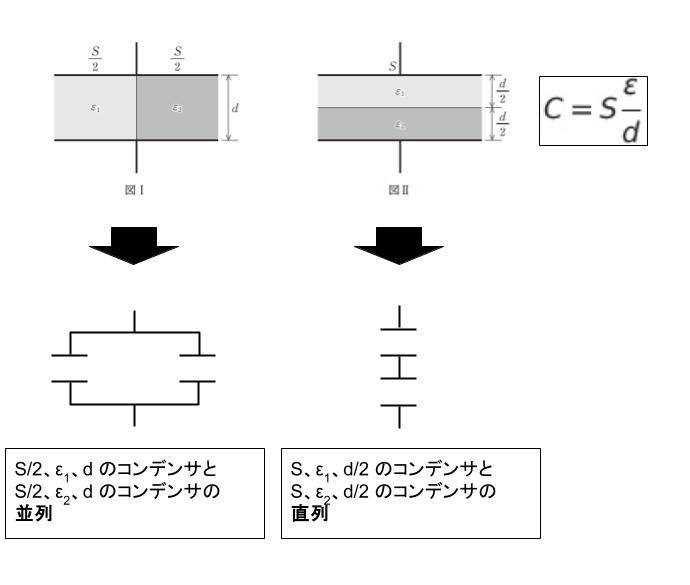
２つの「直列」コンデンサがあって、静電容量がそれぞれ C₁,C₂ なら、合成すると C₁・C₂/ (C₁ + C₂) です。２つの「並列」コンデンサがあって、静電容量がそれぞれ C₁,C₂ なら、合成すると (C₁ + C₂) です。

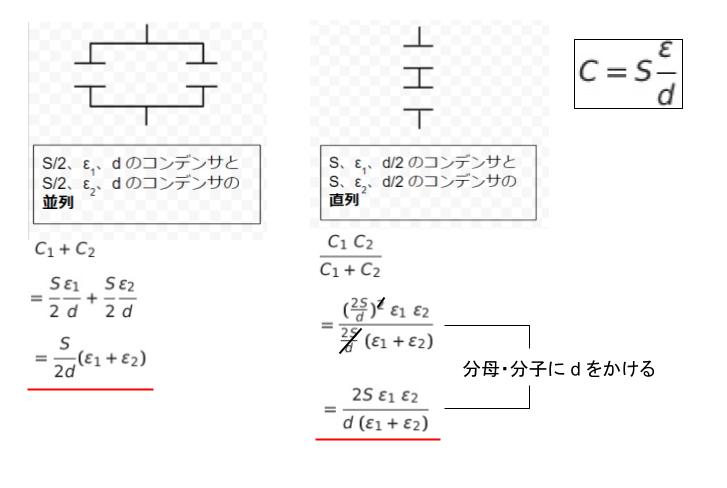
図Ⅰは C₁ = ε₁ × (S/2) /d、C₂ = ε₂ × (S/2) /d の 2 つのコンデンサの並列と考えます。並列は足せばいいので、C_Ⅰ = S(ε₁ + ε₂)/2d です。正解は 1 or 2 です。

図Ⅱは C₁ = ε₁ × S/(d/2)、C₂ = ε₂ × S/(d/2) の 2 つのコンデンサの直列と考えます。合成すると、C_Ⅱ = 2S(ε₁ ε₂)/d(ε₁ + ε₂) です。C_Ⅰ、C_Ⅱ の計算過程はそれぞれ以下のようになります。

以上より、正解は 2 です。

類題 H24 no21 コンデンサ
https://yaku-tik.com/koumuin/h24-denjyou-21/