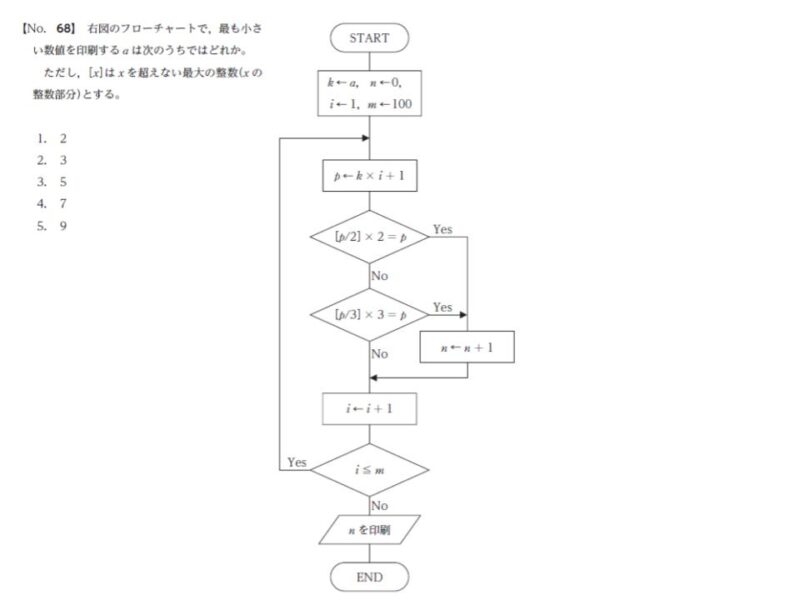
問 題
解 説
具体的に選択肢 1 の a = 2 でチャートを読んでいきます。
(k,n,i,m) = (2,0,1,100)
(k,n,i,m,p) = (2,0,1,100,3) [3/2] → 1 なので n、[3/3] → 1 なので y
(k,n,i,m,p) = (2,1,2,100,3) 2 ≦ 100 なので y
(k,n,i,m,p) = (2,1,2,100,5) [5/2] → 2 なので n、[5/3] → 1 なので n
(k,n,i,m,p) = (2,1,3,100,5) 3 ≦ 100 なので y
(k,n,i,m,p) = (2,1,3,100,7) [7/2] → 3 なので n、[7/3] → 2 なので n
・
・
・
と進んでいきます。
チャートは以降
i が 1 ずつ増えていき i が 101 になるまでぐるぐる回ります。
p:2 × i + 1 が 「2 で割れきれる」or 「3 で割れきれる」場合に n の値が 1 増えます。ここで「2 × i + 1」 は必ず奇数です。2 で割り切れることはありません。
従って
p = 3,9,15… の時に n が 1 増えます。これは i = 1,4,7,… に対応します。
i は 101 までぐるぐる回るので
i = 1,4,7,…,100 の時、計 34 回 n が増えます。つまり、最後に n = 34 が出力されます。以上が a = 2 の場合です。
もしも a の値が 奇数であれば、i が奇数の時に「奇数 × i (奇数) + 1」が偶数になります。すると i が 1,3,5,,,99 で必ず n が増えることから、n が 50 よりも大きくなります。
従って
最も小さい数値を印刷する a は、選択肢の中であれば 唯一偶数である「2」です。
以上より、正解は 1 です。

コメント