問 題
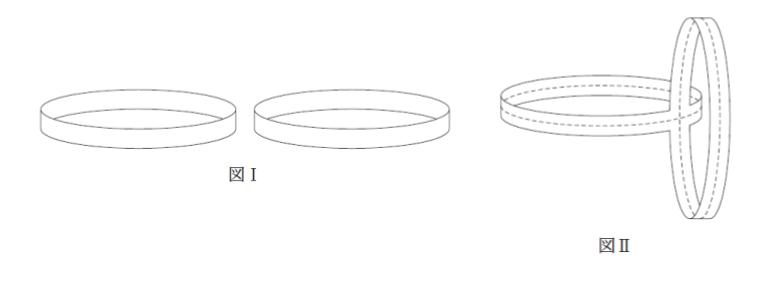
図Ⅰのように,幅が一定の紙テープを用いて同じ大きさの輪を二つ作り,図Ⅱのように,二つの輪が直交するようにこれらを面で接着した。この接着した二つの輪を,その中央線(図Ⅱの点線)に沿って切り開いたとき,できる図形として最も妥当なのはどれか。

正解 (5)
解 説
こういう問題は、頭の中でさくさく切れる人もいると思いますが、そうでない人は一部分に注目して、選択肢消去が定石です。
本問では、点線部分を切っていくと、できる図形には、直角部分が4つ外側にできると考えられます。下図における赤で示した部分です。従って、直角が4つない選択肢 3 は誤りです。
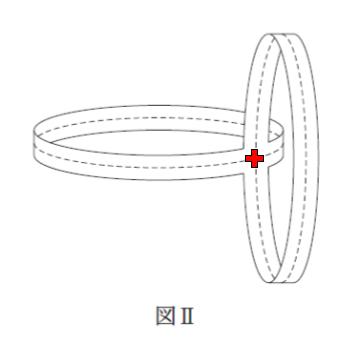
ある直角から次の直角まで点線を追っていくと、ちょうど円一周となります。一例としては下図になります。
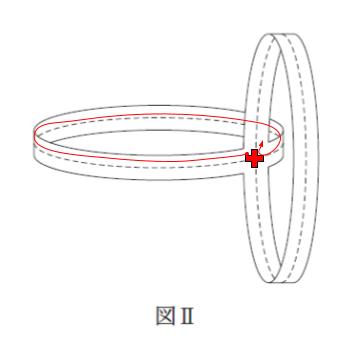
直角から次の直角まではどれも円周なので同じ長さとわかります。つまり、できる図形の直角から直角までの長さはどれも同じはずです。従って、選択肢 1,4 は誤りです。
そして、ある直角から次の直角まで切っていって広げれば、その部分は明らかに直線になると考えられます。つまり、直線→直角→直線・・・という流れで書ける図形です。従って、選択肢 2 は誤りです。
以上より、正解は 5 です。

コメント