問 題
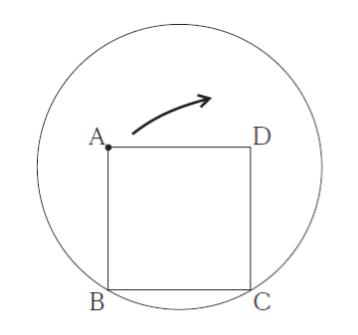
図のように,円の内側に一辺の長さが円の半径に等しい正方形 ABCD がある。この正方形ABCD が円の内側に沿って矢印の方向に滑ることなく回転しながら移動するとき,頂点Aの描く軌跡として最も妥当なのはどれか。
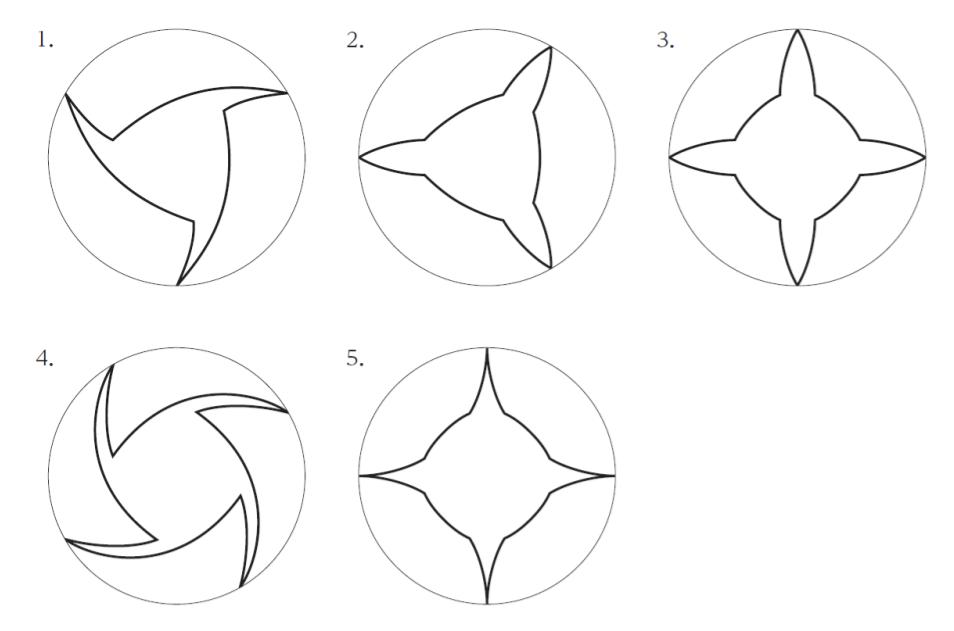
正解 (2)
解 説
軌跡は1点に注目し、選択肢の消去法が定石です。(参考 H30no18)。本問では頂点 A の軌跡が問われているため、点 A に注目します。
転がっていく方向において、一番先頭の地面と接している点が回転の中心となります。最初の回転の中心は C です。CA を半径として、点 A の軌跡は以下のようになります。
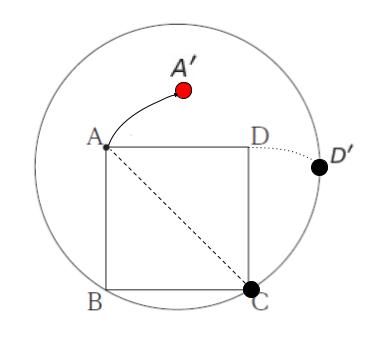
次に、D’ が回転の中心となり、D’A’ を半径として円の一部を描きます。
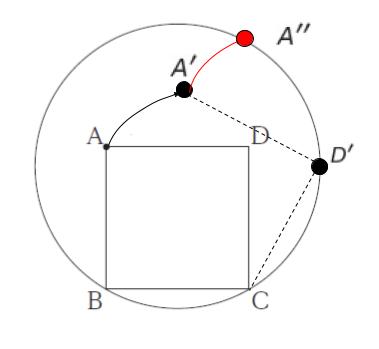
到達点は円の右上あたりとわかります。従って、選択肢 3,5 は右上あたりに軌跡がないため誤りです。
また、点 A の右上までの軌跡は、回転半径が CA →D’A’ なので、半径の異なる2つの円の一部です。従って、滑らかにはつながりません。D’A’ の方が半径が明らかに短く、そのため軌跡は後半ポコっとはねます。従って、選択肢 1,4 は右上までの軌跡部分が滑らかなので、誤りです。
以上より、正解は 2 です。

コメント