問 題
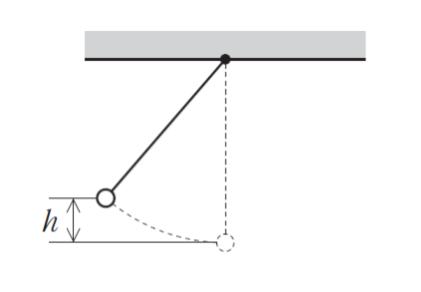
図のように,糸の一端を天井に固定し,他端に小球を取り付けて,糸がたるまないように,この小球を最下点から高さ h の位置まで持ち上げ,静かに放したところ,小球は運動を始めた。エネルギー保存の法則を用いると,小球が最下点を通過するときの小球の速さとして最も妥当なのはどれか。ただし,重力加速度の大きさを g とする。

正解 (2)
解 説
力学的エネルギー = 位置エネルギー+運動エネルギーです。これは摩擦力などが働かない限り保存されます。本問において、高さ h の位置まで持ち上げた時点における力学的エネルギー = 最下点を通過する際の力学的エネルギー が成立します。
位置エネルギー U = mgh です。
小球の重さを m とします。高さ h の位置まで持ち上げた時点において、U = mgh です。
運動エネルギー K = mv2/2 です。高さ h の位置まで持ち上げた時点において、v = 0 なので、運動エネルギーは0です。
最下点を通過する際
位置エネルギーは0です。運動エネルギーは、通過する速さを v とおけば、mv2/2 です。
力学的エネルギー保存より
mgh + 0 = 0 + mv2/2 です。v について解けば、v = √2gh となります。(選択肢からわかっていたのですが、速さは小球の重さによらないとわかります。つまり、ピンポン玉だろうが、ボーリングの玉だろうが、同じ高さまで持ち上げた場合、最下点における速さは 同じということです。地味に面白い結果ではないでしょうか。)
以上より、正解は 2 です。
類題 H30no52

コメント