問 題
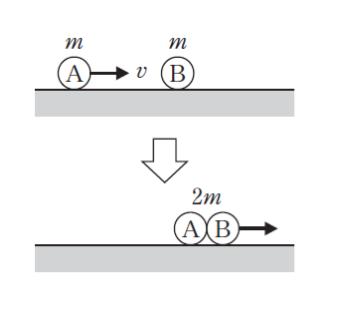
図のように,滑らかな水平面の一直線上を速さ v で運動している質量 m の小球 A が,同一直線上に静止している質量 m の小球 B に衝突したところ,衝突後,二つの小球は一体となり,質量 2m の小物体 AB として運動した。このとき,一体となった小物体 AB の速さとして最も妥当なのはどれか。
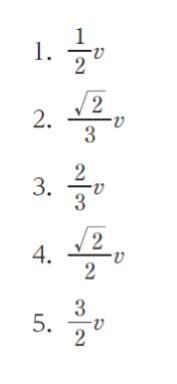
正解 (1)
解 説
衝突と来たら「運動量保存則」を考えます。運動量とは、質量 × 速さです。衝突の前後で、運動量は保存されます。
【衝突前】
小球 A の持つ運動量:m × v
小球 B の持つ運動量:m × 0 = 0
合計:mv + 0 = mv
【衝突後】
一体となった小物体 AB の持つ運動量:2m × ?
衝突前と衝突後の運動量が保存される、つまり等しい ため
mv = 2m × ? です。選択肢 を見ると、v/2 を代入すれば、等式が成り立ちます。
以上より、正解は 1 です。

コメント