問 題
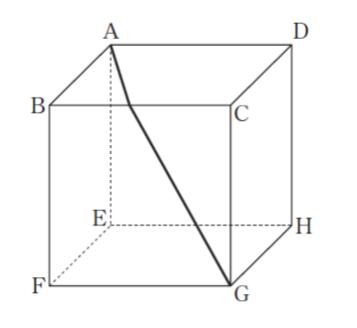
図のような立方体 ABCD ‒ EFGH の周りに,点 A から点 G まで辺 BC と交わるように糸を巻き付けた。この糸の長さの最小値が10 であるとき,この立方体の一辺の長さはいくらか。
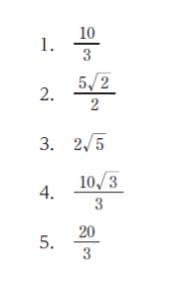
正解 (3)
解 説
点 A → BC 上の点 → G と通過する糸に関する問題です。立体のままではわからないため、展開図を考えます。色を付けた2面のみに注目します。展開図において AG を結んでできる線分が最短距離です。そのため、線分 AG の長さが、糸の長さの最小値である 10 とわかります。
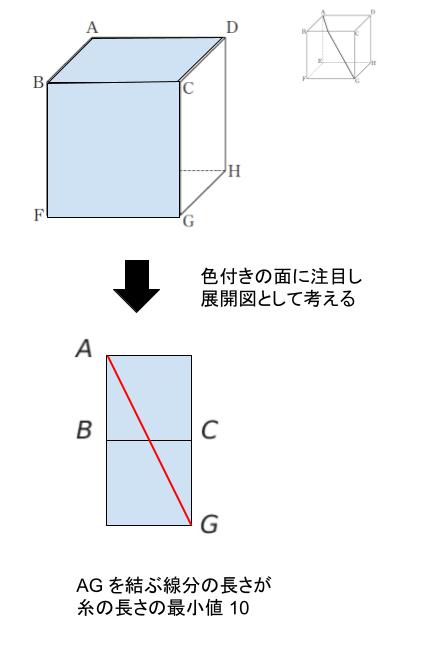
すると、立方体の一辺の長さを a とすれば、三角形 AFG は 直角を挟む2辺は a,2a です。三平方の定理から、AG は √5 a と表されます。計算は以下のようになります。
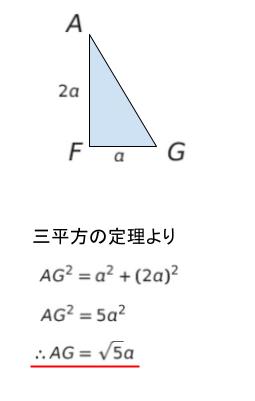
√5a = 10 なので、a = 2√5 です。
以上より、正解は 3 です。

コメント