公務員試験 2019年国家一般職(土木) No.24解説

　問題　　　　　

正解 (2)

　解説　　　　　

・重心位置に外力 P ならば σ_c = ーP／A です。中空円形なので外側の円ー内側の円を計算すれば A = πd²/4 ー πd²/16 = 3πd²/16 です。

・偏心荷重の場合
重心位置の場合の応力に加えて「曲げ応力」が加わります。曲げ応力は、±M／I　× y です。I は断面二次モーメントです。中空円形なので I = (π/64) × {d⁴ – (d/2)⁴} です。

引張側の最大応力は
y = d/2 の時、(M／I) × d/2 です。

M は荷重によるモーメントです。
モーメントは「力 × 距離」なので、直径を d とすれば M = P × 3d/8 です。

これらを代入して整理すると 112P/15πd² を得ます。計算の一例が以下の通りです。

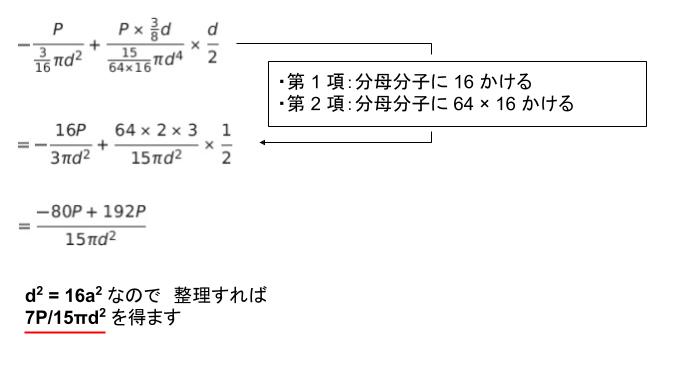
以上より、正解は 2 です。

コメント