公務員試験 2019年 国家一般職(土木) No.23解説

　問 題　　　　　

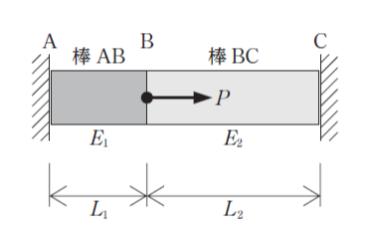
図のように、材質がそれぞれ一様で断面積は互いに等しい棒 AB、棒 BC が固定壁間に隙間なく接合されている。AB、BC の境目にある点 B の断面中心に軸方向荷重 P を右向きに作用させたとき、AB に作用する軸力の大きさとして最も妥当なのはどれか。

ただし、AB、BC の自重及び P による断面積変化は無視でき、AB、BC のヤング係数をそれぞれ E₁、E₂、長さをそれぞれ L₁、L₂ とする。

 

 

 

 

 

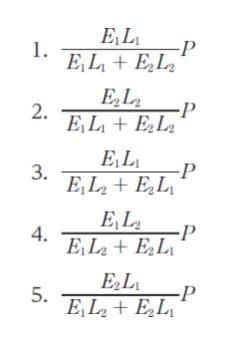
　解 説　　　　　

【ひずみに関する基礎知識】

力を加えて、元々 長さ l の物体が Δl 伸びた時、ひずみ ε を Δl/l で表します。この時、E をヤング係数（ヤング率）として、σ = Eε が成立します。σ は軸応力です。軸方向力を P、断面積 A とすると、軸応力 σ は P/A です。

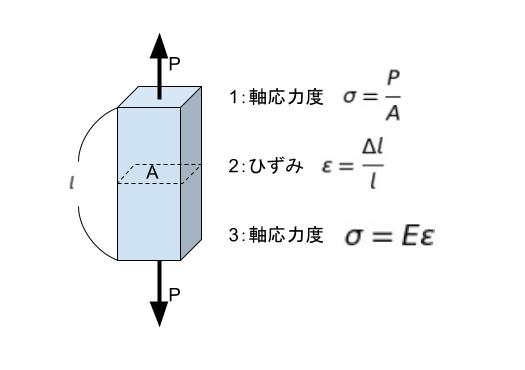
本問では 棒 AB が伸び、棒 BC が縮みます。この時の変化量を Δl とします。また、壁の両端における反力をそれぞれ P_A、P_B とします。すると P = P_A + P_B …(1) です。

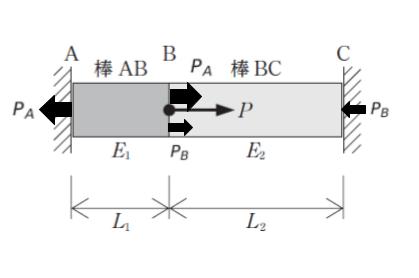
棒 AB のひずみは ε_AB = Δl/L₁
棒 BC のひずみは ε_BC = Δl/L₂ です。

軸応力の式を変形すれば P = Aσ なので P_A、P_B はそれぞれ
P_A = AE₁ε = AΔl × E₁/L₁ 
P_B = AE₂ε = AΔl × E₂/L₂ と表せます。AΔl は共通なので

P_A：P_B = E₁/L₁：E₂/L₂ です。内項の積＝外項の積なので
P_A × (E₂/L₂) = P_B × (E₁/L₁)…(2) です。

  (1) より P_B = P – P_A を代入して整理すれば
P_A = (E₁L₂/(E₁L₂ + E₂L₁) P となります。

以上より、正解は 4 です。

類題 H26 no23
https://yaku-tik.com/koumuin/h26-doboku-23/