公務員試験 2019年 国家一般職(土木) No.19解説

　問 題　　　　　

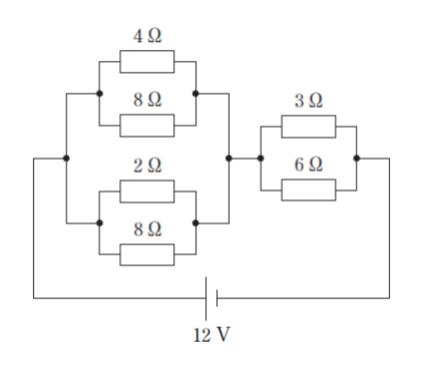
図のような回路において、4 Ω の抵抗で消費される電力はおよそいくらか。

1． 4 W
2． 8 W
3． 12 W
4． 16 W
5． 20 W

 

 

 

 

 

　解 説　　　　　

「２つの並列抵抗の合成」は「分母足す、分子かける」です。

【左半分の 4 つの抵抗の合成】
・左上部：4×8/(4+8) = 32/12 = 8/3
・左下部：2×8/(2+8) = 16/10 = 8/5

そして
8/3 と 8/5 の合成が、なんと ぴったり 1 です。これは気持ちいいので、ぜひ各自確認してみてください！

【右半分の 2 つの抵抗の合成】
・右部：3×6/(3+6) = 2 です。

従って、全ての抵抗を合成すれば、1+2 = 3 Ωです。オームの法則 V = RI より、流れる電流は 4 A とわかります。

左半分の 4 つの抵抗は合成すると 1 Ω、右半分の 2 つの抵抗は合成すると 2 Ω だったので、以下のように簡略化できます。

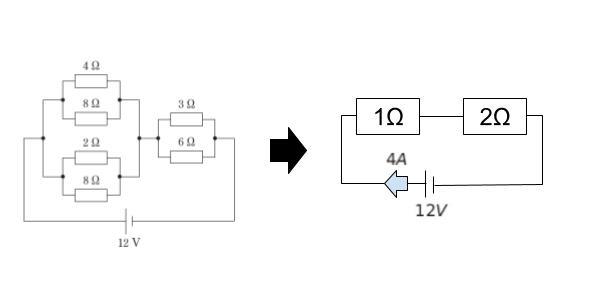
簡略化した回路の 1 Ω の抵抗に注目すれば、V = RI より、かかる電圧は 1 × 4 = 4 V です。並列回路ではかかる電圧が等しいので、元の回路における 4 Ω の所にかかる電圧も 4V とわかります。

電力 P = VI = V²/R なので
求める電力は 4²/4 = 4 W です。

以上より、正解は 1 です。