問 題
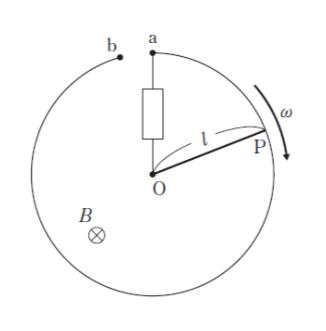
電磁誘導に関する次の記述の ㋐、㋑、㋒ に当てはまるものの組合せとして最も妥当なのはどれか。
「図のように、紙面に対して垂直に表から裏へ向かう、磁束密度の大きさが B の一様な磁界中において、長さ l の細い導体棒 OP と、点 O を中心とする半径 l の円形導線 ab が磁界と垂直に置かれ、抵抗と接続されている。
いま、OP が O を中心に円形導線の円周に沿って、大きさ ω の一定の角速度で時計回りに回転している。このとき、OP に流れる電流の向きは ㋐ である。
また、OP が単位時間当たりに磁界を横切る面積は ㋑ であるため、OP に生じる誘導起電力の大きさは ㋒ である。ただし、誘導電流がつくる磁界は無視するものとする。」
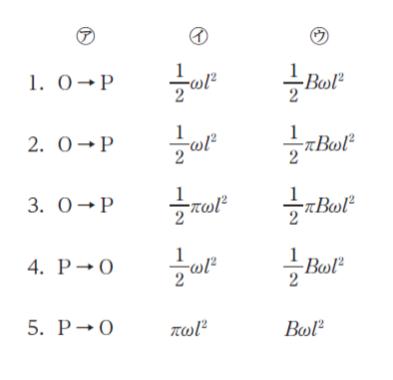
解 説
【レンツの法則】
レンツの法則は、電磁誘導による「誘導電流の向き」に関する法則です。その内容は「磁束の変化を妨げる方に電流が流れる」というものです。
㋐ ですが
時刻が進むと 扇形 OaP の面積が大きくなり、扇形部分を貫く磁束は増加します。この変化を妨げようとするはずです。すると、力が反時計回りに作用するような向きに電流が流れます。フレミングの左手の法則より、流れる電流は O → P 方向です。正解は 1 ~ 3 です。
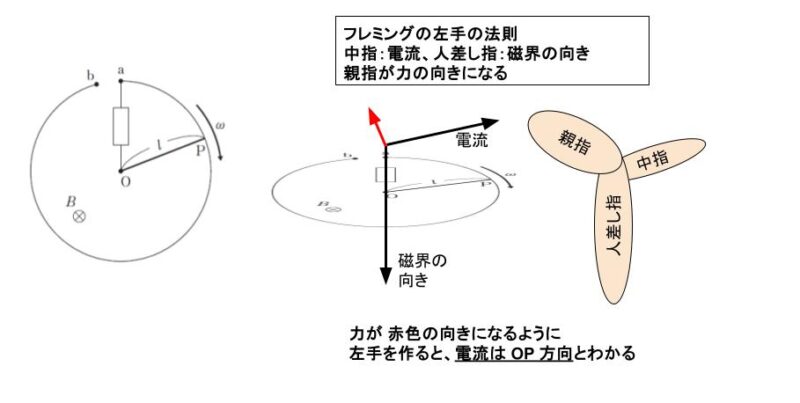
㋑ ですが
半径 l、角速度 ω の時、単位時間当たりで通過する扇形の弧長 が lω、単位時間当たりに通過する扇形の面積が l2ω/2 です。
角速度 ω の単位が [rad/s] なので、単位時間当たりであれば ω [rad] だけ動きます。単位が rad の場合を「弧度法」といい、弧度法で表した際の扇形の弧長と面積は基礎知識です。覚えてしまって OK です。正解は 1 or 2 です。
㋒ ですが
巻数 N のコイルにおいて生じる誘導起電力は、ファラデーの法則より V = N(dΦ/dt)です。本問では N = 1 と考えればよいです。そして Φ = BS なので V = B × (dS/dt) = B × ㋑ でよいと考えられます。
以上より、正解は 1 です。

コメント