問 題
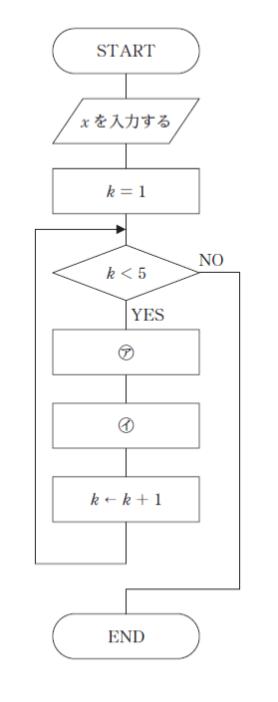
図は正の整数である 10 進数 x (0 < x < 1000) を 4 桁の 8 進数に変換する処理を表すフローチャートである。8 進数は下位桁から順に 1 桁ずつ、配列の要素 a[1] から a[4] に格納される。例えば、x = 83 のとき、a[1] = 3、a[2] = 2、a[3] = 1、a[4] = 0となる。このとき、図中の ㋐、㋑ に当てはまるものの組合せとして最も妥当なのは次のうちではどれか。

解 説
【n 進数の基礎知識】
n 進数の1桁目は n0 が何個あるかを示します。 以下、2 桁目は n1 が何個あるか・・・です。ちなみに、小数点以下の場合、小数点第一位は n-1 が何個あるかを示します。以下、小数点第二位は n-2 が何個あるか・・・を示します。
例の x = 83 は、80 × 3 + 81 × 2 + 82 × 1 なので 桁の小さい方から 3,2,1 つまり 123(8) と表すことができるということです。
10 進数を 8 進数に直すためには、数を 8 で割った余りを逆 L 字で読めばよいです。例の x = 83 の場合、以下のようになります。
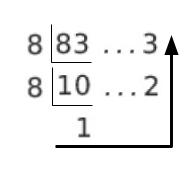
㋐ ですが
10 進数を 8 進数に直す流れを考えれば、a [k] ← k を 8 で割った余り と考えられます。
㋑ ですが
10 進数を 8 進数に直す流れを考えれば、x ← x を 8 で割った商 が妥当です。
※ ㋐ と ㋑ が逆の選択肢 2 でもよいのではないかと感じるかもしれません。しかし選択肢 2 の順序では、例の 83 であれば「83 を 8 で割った 10」に対して「8 で割った余りを x[k] に入れる」となります。つまり、いきなり 2 からになってしまいうまくいきません。
以上より、正解は 5 です。

コメント