問 題
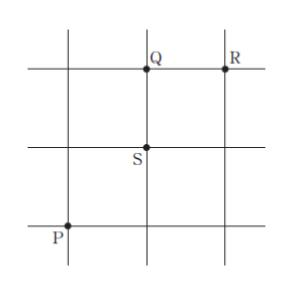
図のように、隣り合う交差点間の距離が等しい道路がある。
A さんは、交差点 P を出発し、最短の経路で交差点 Q へ向かう。B さんは、A さんが交差点 P を出発するのと同時に交差点 R を出発し、最短の経路で交差点 P へ向かう。
二人は、同じ速さで移動し、各交差点において、最短の経路の方向が二つあるときは、等しく確率 1/2 でどちらかに行き、一つしかないときは、確率 1 でそちらに行くものとする。このとき、二人が交差点 S で出会う確率はいくらか。
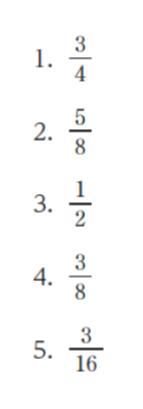
正解 (4)
解 説
【A が P → S と行く確率】
右 → 上 と行く場合と
上 → 右 と行く場合の確率の和です。
初めに右に行けば、次に確実に上に行くので、この確率は
1/2 × 1 = 1/2 です。
初めに上に行けば、1/2 で 右に行くので、この確率は
1/2 × 1/2 = 1/4 です。
従って
1/2 + 1/4 = 3/4 …(1) です。
【B が R → S と行く確率】
左 → 下 と行く場合と
下 → 左 と行く場合の確率の和です。
初めに左に行けば、1/2 で 下に行くので、この確率は
1/2 × 1/2 = 1/4 です。
初めに下に行けば、1/2 で 左に行くので、この確率は
1/2 × 1/2 = 1/4 です。
従って
1/4 + 1/4 = 1/2 …(2) です。
【A,B が 交差点 S で出会う確率】
(1) かつ (2) の確率なので
3/4 × 1/2 = 3/8 です。
以上より、正解は 4 です。

コメント