問 題
実数 x,y が cos (x – y) = 0 を満たすとき、cos x + cos y の最大値はいくらか。
1. 1
2. √2
3. 3/2
4. √3
5. 2
正解 (2)
解 説
まず、三角関数なので「単位円による定義」を思い出します。これは基礎知識です。
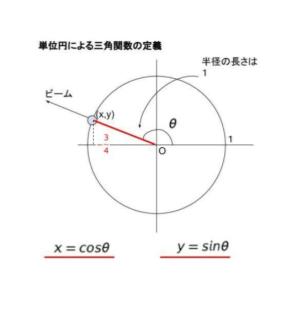
cos θ が 0 になる時は、ビームとぶつかる点の x 座標が 0 なので、θ = 90° or 270°です。± 90° といえます。x – y = ± 90° なので x = y ± 90° であればよいとわかります。
cos θ の値が、cos x、cos y 共に正である方が、和は大きいと考えられます。x = -90°、y = 0° から x = 0°、y = 90° までを考えればよさそうです。後は有名角で具体的に考えます。
x = -90°、y = 0°
→ cos x = 0、cos y = 1 → 和が 1
x = -60°、y = 30°
→ cosx = 1/2 、cos y = √3/2 → 和が (1+√3)/2
x = -45°、y = 45°
→ cosx = √2/2、cosy = √2/2 → 和が √2
x = -30°、y = 60° → 和が (1+√3)/2
x = 0°、y = 90° → 和が 1 です。
この中で最大 は 和が √2 です。
これ以上は作れなさそうです。
以上より、正解は 2 と考えられます。

コメント