問 題
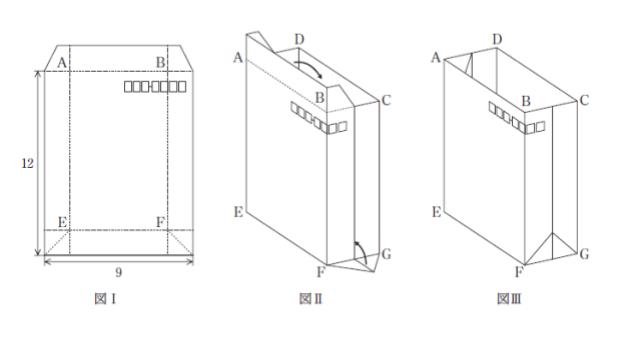
図Ⅰのような縦の長さ 12、横の長さ 9 の封筒を点線に沿って図Ⅱのように折り、図Ⅲのような直方体の形をした箱 ABCD ‒ EFGH を作る。この箱の容積が最大になるような EF の長さはいくらか。ただし、封筒の紙の厚みは無視する。
1. 2
2. 3
3. 4
4. 5
5. 6
正解 (4)
解 説
組み立てた後の図Ⅲにおいて、AB を「横」、AD を「縦」、AE を「高さ」とします。AB = EF です。
図Ⅰ~ 図Ⅲを見れば、まず横の長さ AB は EF の長さと同じです。次に縦の長さ AD は「(9 – 横)」です。 高さは「12 – AD/2」です。
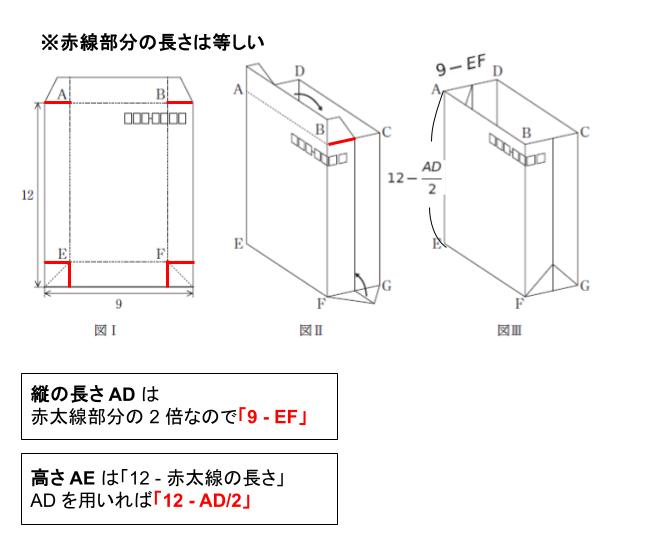
具体的に考えるのがおすすめです。
選択肢 1 が正解と仮定します。
EF = 2 の時、AB = 2、AD = 9 – 2 = 7、AE = 12 – 3.5 = 8.5 です。体積は 119 です。
選択肢 2 が正解と仮定します。
EF = 3 の時、AB = 3、AD = 9 – 3 = 6、AE = 12 – 3 = 9 です。体積は 162 です。
選択肢 3 が正解と仮定します。
EF = 4 の時、AB = 4、AD = 9 – 4 = 5、AE = 12 – 2.5 = 9.5 です。体積は 190 です。
選択肢 4 が正解と仮定します。
EF = 5 の時、AB = 5、AD = 9 – 5 = 4、AE = 12 – 2 = 10 です。体積は 200 です。これが最大です。
選択肢 5 が正解と仮定します。
EF = 6 の時、AB = 6、AD = 9 – 6 = 3、AE = 12 – 1.5 = 10.5 です。体積は 189 です。
以上より、正解は 4 です。

コメント