問 題
あるじゃんけんマシンがある。このじゃんけんマシンが出す手は、グー、チョキ、パーのいずれかであり、その直前に出した手にのみ依存し、その法則性は以下のとおりである。
・グーの次は、1/2 の確率でチョキを出し、1/2 の確率でパーを出す。
・チョキの次は、1/4 の確率でグーを出し、1/2 の確率でチョキを出し、1/4 の確率でパーを出す。
・パーの次は、1/4 の確率でグーを出し、1/4 の確率でチョキを出し、1/2 の確率でパーを出す。
十分な回数の勝負が行われた後、各手を出す確率がそれぞれ一定の値になったときのグーを出す確率はいくらか。
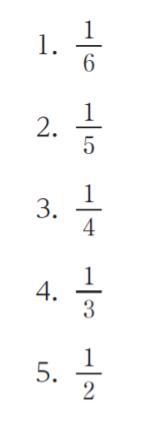
解 説
各手を出す確率が一定になった時の チョキの確率を x、パーの確率を y とします。グーの確率は 1 – (x+y) と表せます。※ 後の計算を考えて、少し工夫した置き方にしていますが、グーを x、パーを y、チーを 1 – (x+y) でもかまいません。
次の回のじゃんけんにおいて、グー、チー、パーの出る確率は 以下のようにまとめることができます。
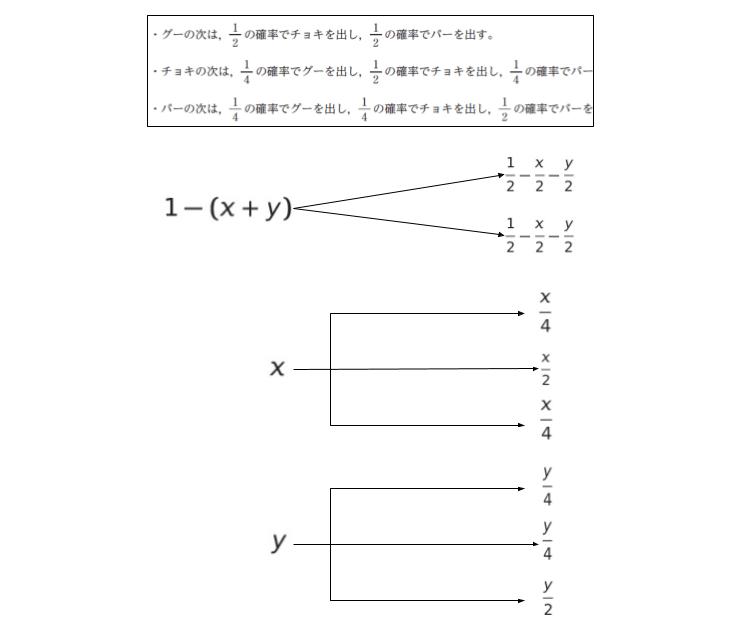
「次の回のじゃんけんの チョキの確率」
に注目すると (1/2 – x/2 – y/2) + x/2 + y/4 です。整理すれば 1/2 -y/4 となります。これが前回のチョキの確率である x と等しいため『x = 1/2 – y/4』・・・(1) です。
「次の回のじゃんけんの パーの確率」
に注目すると (1/2 – x/2 – y/2) + x/4 + y/2 です。整理すれば 1/2 -x/4 となります。これが前回のパーの確率である y と等しいため『y = 1/2 – x/4』・・・(2)です。
(1),(2) の辺々足せば
(x+y) = 1 -(x+y)/4
∴ (x+y) = 4/5 です。
従って
グーの確率 1-(x+y)
= 1-4/5
= 1/5 となります。
※(1),(2) から x = y = 2/5 と求めてから、グーの確率を出しても、もちろんかまいません。答えが出れば 何でも OK です。
以上より、正解は 2 です。

コメント