問 題
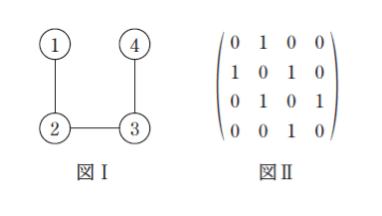
次の ㋐ ~ ㋓ は、頂点 1 ~ 5 をもつグラフを隣接行列で表したものである。グラフを構成する全ての辺をちょうど 1 回ずつ通る経路が存在するものを表した隣接行列のみを挙げているのはどれか。

ただし、隣接行列の x 行 y 列目の成分は、頂点 x と y を結ぶ辺の数であり、例えば、図Ⅰのグラフを隣接行列で表すと図Ⅱのようになる。
1.㋐、㋑
2.㋐、㋒
3.㋐、㋓
4.㋑、㋒
5.㋒、㋓
正解 (2)
解 説
【一筆書き の基礎知識】
一筆書きの『途中の点』は「入ってきたら出ていく」はずだから、頂点から出ている線の数は偶数です。奇数の点は始点 もしくは終点にしかなりません。さらに始点かつ終点である点については、頂点から出ている線の数がやはり偶数になります。
以上をまとめると、一筆書きができる図形は、奇点が0 or 2 です。(オイラーの定理)。そして、奇点が2つの場合、その2つが始点及び終点です。
「全ての辺を 一度ずつ通る」を一筆書きと読み替えれば、後は行列から奇点の数を読み取る問題となります。行列のある 1 行に注目して、1 の個数が その頂点から出ている辺の数です。
㋐ の行列に注目すれば
全ての行において 1 が 2 個です。
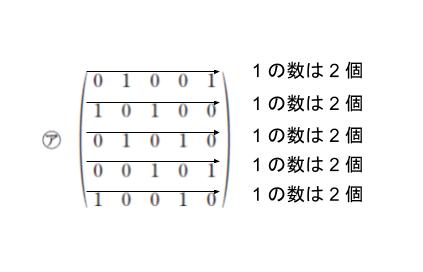
これは全ての頂点から 2 本線が出ているということです。つまり全て 偶点であり、奇点が 0 と読み取れます。従って、一筆書き可能です。㋐ は妥当です。
同様に読み取れば、㋑、㋓ は奇点 4 個で一筆書き無理です。㋒ は奇点 2 個で一筆書き可能です。
以上より、正解は 2 です。
類題 H30 no34 グラフ
https://yaku-tik.com/koumuin/h30-denjyou-34/

コメント