問 題
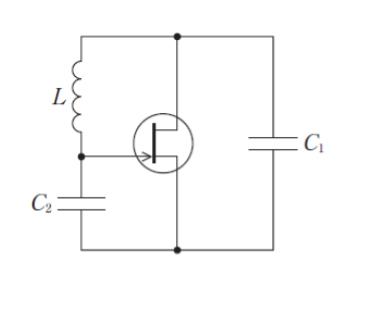
図は、電界効果トランジスタ、インダクタンス L のコイル、キャパシタンス C1、C2 の二つのコンデンサからなるコルピッツ発振回路の原理回路を示している。この回路は、コイル及び二つのコンデンサの作る直列合成インピーダンスが零となる周波数で発振する。この回路の発振周波数として最も妥当なのはどれか。
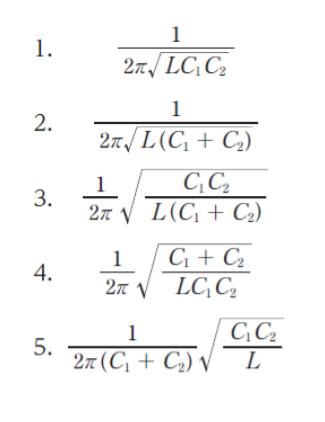
解 説
発振回路は、自分自身で交流信号を持続的に出力する回路のことです。代表的なものとして、クラップ発振回路や本問のコルピッツ発振回路などがあります。発振回路についての知識は本問の解答には不要です。
インダクタンス L のコイル、キャパシタンス C1、C2 の二つのコンデンサが直列につながっているので、インピーダンスを考えます。まずは 2 つのコンデンサについて、1 つに合成します。
【コンデンサの合成 基礎知識】
・C1、C2 のコンデンサ「直列」合成
→ C1・C2/(C1 + C2)
・C1、C2 のコンデンサ「並列」合成
→ C1 + C2 です。
本問は直列なので
C1・C2/(C1 + C2) ・・・(1) と合成できます。
問題文より、インピーダンスの公式における「コイルとコンデンサの項の和」が 0 になる時が発振条件です。すなわち、(ωL – 1/ωC)2 = 0 → ωL = 1/ωC が発振条件です。
発振条件の C に (1) を代入して ω = … の形に解けばよいです。ω2 = 1/L × (C1・C2/(C1 + C2) ) となります。ここで 2πf = ω に注意します。本問で最終的に求めたいのは「発信周波数 f」なので f = ω/2π です。計算過程は以下のようになります。
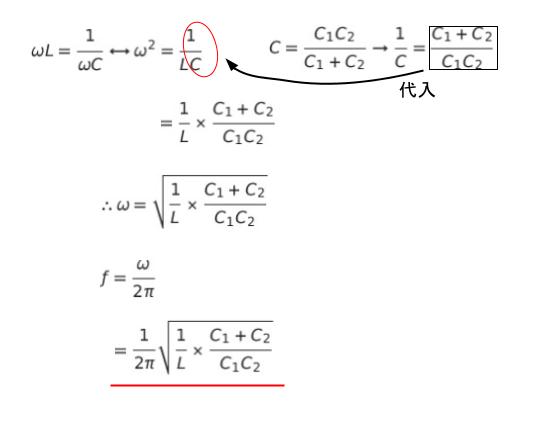
以上より、正解は 4 です。
類題 国家一般職 高卒技術 H26no25
https://yaku-tik.com/koumuin/h26-gijyutu-25/

コメント